Dr. Meiss Collaborates on Researching Nuclear Fusion Power, Research Effort Awarded Prestigious Simons Grant
Dr. Meiss, Professor of Applied Mathematics, is one of ten principle investigators (PIs) awarded a prestigious grant from the Simons Foundation to research optimal stellarator designs. The Simons Grant will be $2million USD a year for four years.
The research is led by Princeton University and is a collaboration between Australian National University, Columbia University, Cornell University, Max Planck Institute for Plasma Physics Greifswald, New York University, University of Colorado at Boulder, University of Maryland, University of Texas at Austin, and Warwick University. The ten PIs make up an interdisciplinary team of experts in magnetic fieldline flow, particle confinement, magnetohydrodynamics, and multi-objective stochastic optimization.
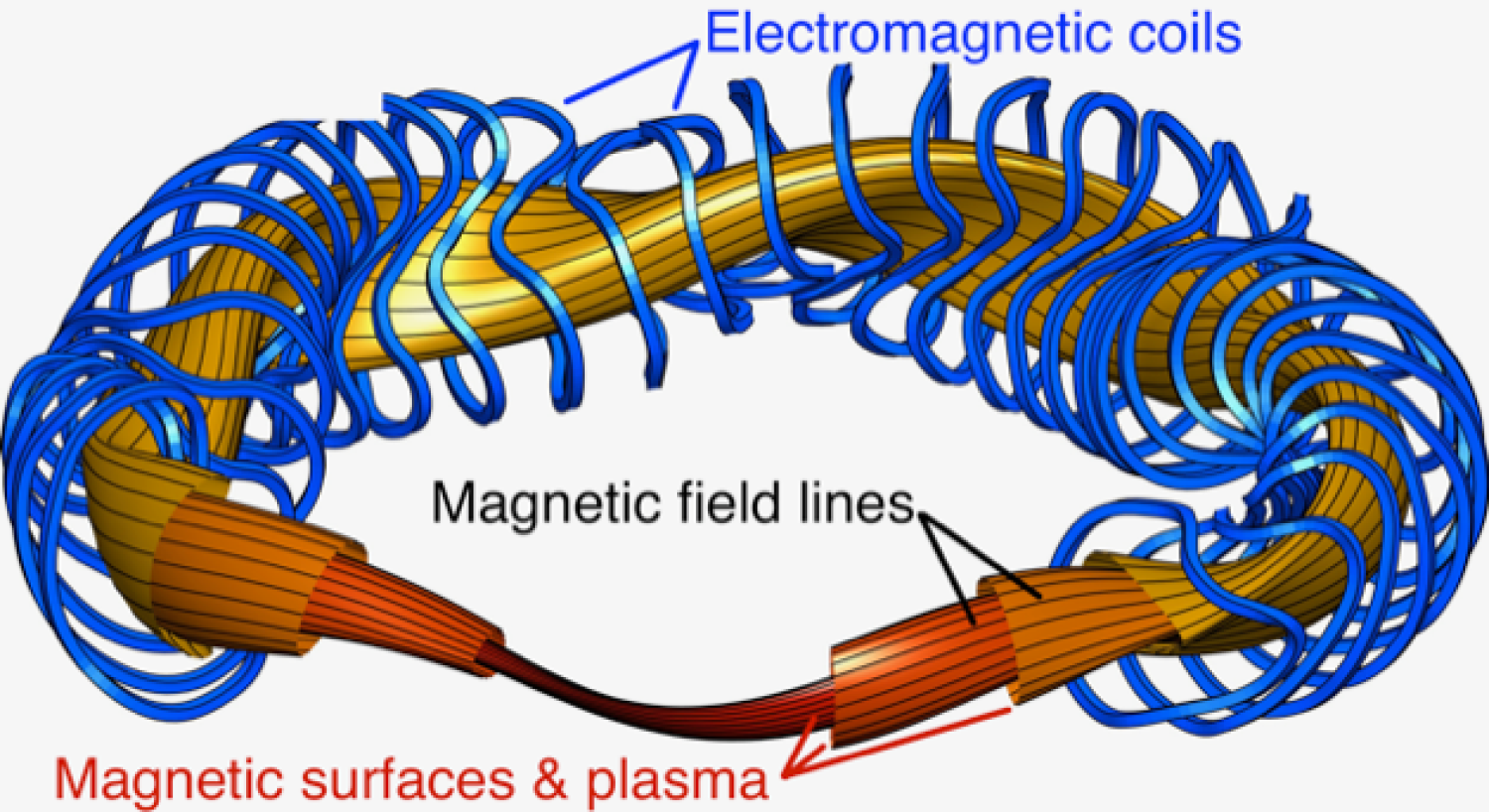
A general outline of a stellarator’s electromagnetic coils, magnetic field lines, magnetic surfaces, and plasma are shown in the image. This image is courtesy of the Max Planck Institute for Plasma Physics.
Stellarators are devices that could potentially generate sustained and controlled nuclear fusion power. According to Time Magazine’s 2010 article, “10 Questions for Stephen Hawking,” when asked about the one scientific advancement he’d like to see in his lifetime, Hawking responded, “I would like nuclear fusion to become a practical power source. It would provide an inexhaustible supply of energy, without pollution or global warming.”
The goal of a magnetic confinement devices, like the stellarator, is to use magnetic fields to confine hot plasma in order to sustain a nuclear fusion reaction (the fusion of two Hydrogen nuclei to form Helium and release a large amount of energy). For a fusion reaction to occur, the electrostatic repulsion between atomic nuclei must be overcome by heating the particles involved to tens of millions of degrees--turning them into plasma. These devices take advantage of the charges of the particles to contain the plasma using magnetic fields; the plasma particles move around the magnetic field lines in helical orbits, resulting in confinement transverse to the field.
Stellarators have not always been the focus for fusion power devices. Currently, most experimental devices are tokamaks because the design of stellarators has been considered impractical. However, there has been a renewed interest in stellarator designs because (1) the advancement of computer aided design tools now allows for complex stellarator magnet construction, and (2) the stellarator is considered more stable than tokamaks.
According to Dr. Meiss, the tokamak is an axisymmetric torus (bagel-shaped) and uses two magnetic fields to contain the plasma: toroidal (long axis) fields, and poloidal (short axis) fields. The toroidal fields are created by external coils while the poloidal fields arise from the contained plasma’s current. These currents can’t be easily maintained at steady state and also lead to instabilities of the plasma. The stellarator, on the other hand, is not axisymmetric: it is shaped more like a French cruller. The plasma-confining magnetic field is mostly created by external coils, meaning the stellarator has the potential to continuously produce power while avoiding the plasma current-based instabilities of the tokamak. Optimally designing the external coils of the stellarator is one question that Dr. Meiss and other collaborators on the Simons grant plan to answer.
According to Dr. Meiss, he and Dr. Robert MacKay (University of Warwick) lead portion of the project focusing on the use of magnetic fields in the stellarator to confine charged particles geometrically (focusing on imposing approximate symmetries) and dynamically (focusing on the drifting of particles from magnetic surfaces). Given its shape, the fieldlines in the stellarator vary in strength and direction. This variation means particles can drift across magnetic field lines; however, such drifts can be minimized by careful design. According to Dr. Meiss, “if the strength of the magnetic field has a symmetry (even if its direction does not), then Noether’s theorem gives an invariant. We call this ‘quasi-symmetry.’”
Overall, the research on stellarators, as funded by the Simons Foundation grant, plans to answer questions such as, “how do approximate symmetries and quasi-symmetries interact?” “Are there other hidden symmetries that can lead to invariants?” “How can the external coils of the stellarator be optimally designed?”