Astronomy Info

View of the night sky.
Current Events
- This Week's Sky at a Glance from Sky & Telescope
- The Sky This Week from Astronomy Magazine
- Heavens Above Interactive Sky Chart
- Solar System Exploration - What's Up video series
- Latest Sun images from SOHO
- Current Solar Images from the Solar Dynamics Observatory
- NOAA Today's Space Weather with Solar X-Ray Flux & K-Indices
- Moon phases
- SpaceWeather with sunspot numbers and What's Up in Space
- Auroral Activity Maps 3 day forecast from the Space Weather Prediction Center
- Astronomy Picture of the Day from NASA (beautiful images that inspire you to learn something new every day)
- NASA
Annual Solar & Lunar Tables for Boulder
- 2018 Sunrise & Sunset Times in Boulder, Colorado
- 2018 Twilight Times - Civil, Nautical, Astronomical
- 2018 Moonrise & Moonset Times in Boulder, Colorado
Solar Elongations (Angular Separation from the Sun)

Solar Elongations (Angular Separation from the Sun) diagram
Superior planets (those that lie further from the Sun than us: Mars, Jupiter, Saturn, Uranus, Neptune, and Pluto) can reach an elongation of 180 degrees, which is called opposition; that is, they appear in the sky in a direction directly opposite the Sun. At such times, the planet rises as the Sun sets, and sets as the Sun rises. Generally, this is also the time when the planet is closest to the Earth (ignoring minor effects from the eccentricities and tilts of the orbits), since both are on the same side of the Sun. And, because they are nearer, they also appear larger in telescopes and (at least somewhat) brighter in the sky.
Superior planets can experience a conjunction with the Sun, when the elongation goes to zero. Such a conjunction is pretty much an astronomical "non-event", since the planet is completely lost in the glare of sunlight.
Inferior planets (those that lie closer to the Sun than the Earth: Venus and Mercury) never appear in the sky very far from the Sun, and can never lie opposite it. Instead, they reach greatest elongations, either east or west of the Sun, which are the times (again, ignoring the effects of orbital tilts and eccentricities - and the tilt of the Earth's axis as well) for best viewing of these planets. An eastern elongation implies that the planet will be visible after the Sun has set in the west (an "evening star"), while a western elongation implies that the planet appears in the morning sky as a "morning star" before the Sun rises.
Because it is extremely difficult to see any planet when its elongation is less than 18 degrees from the Sun, the inner planet Mercury is only rarely visible to Earth observers: only near times of greatest elongation, and when other conditions - such as when the tilt of the ecliptic (the apparent path of the Earth around the Sun) - makes the planet stand high in the sky away from the glow of twilight.
The inferior planets undergo two different conjunctions with the Sun: a so-called inferior conjunction, when the planet passes directly between us and the Sun; and superior conjunction, when the planet is on the diametrically opposite side of the Sun. Neither of these events are visible, since they are lost in sunlight. However, near (but not at) inferior conjunction, the planet's phase appears as a thin crescent as seen from Earth, while near superior conjunction, the planet appears gibbous (nearly fully illuminated).
Apparent Diameters (Angular Size)
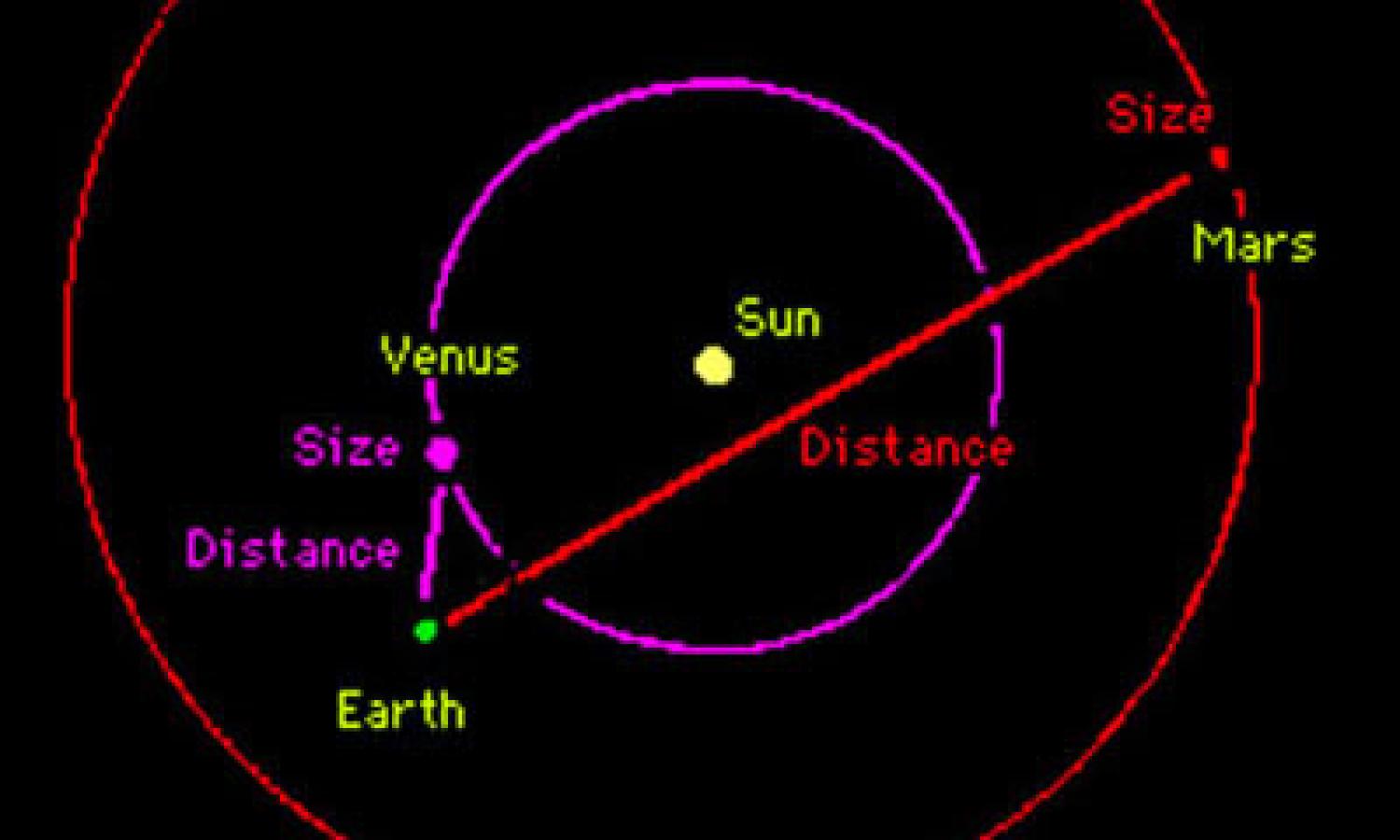
Apparent Diameters (Angular Size) diagram
The three nearest planets - Venus, Mars, and Mercury - undergo dramatic changes in apparent size as our respective orbits alternately bring us closer to or farther from them. Jupiter, at about 5 times the average Earth-Sun distance (called an astronomical unit, or "AU"), also exhibits an apparent change in size because its distance from us can be as little as 4 AU or as great as 6 AU - depending upon whether it's on the same or opposite side of the Sun. But for the outer planets, the effect of the Earth's motion around the Sun - towards or away from it - becomes increasingly insignificant.
As mentioned previously, it is around the time of opposition (for an outer planet) or inferior conjunction (for an inner planet) when that planet's diameter appears largest to us. However, for Mercury and Venus, we can't really see that large diameter because we're viewing the non-illuminated side of the planet in the direct glare of sunlight.
We should mention that the data for Saturn reflects only the size of the ball of the planet itself, not the rings - so the view of Saturn is actually far more spectacular than indicated in the chart.
Phases (Percent Illumination)
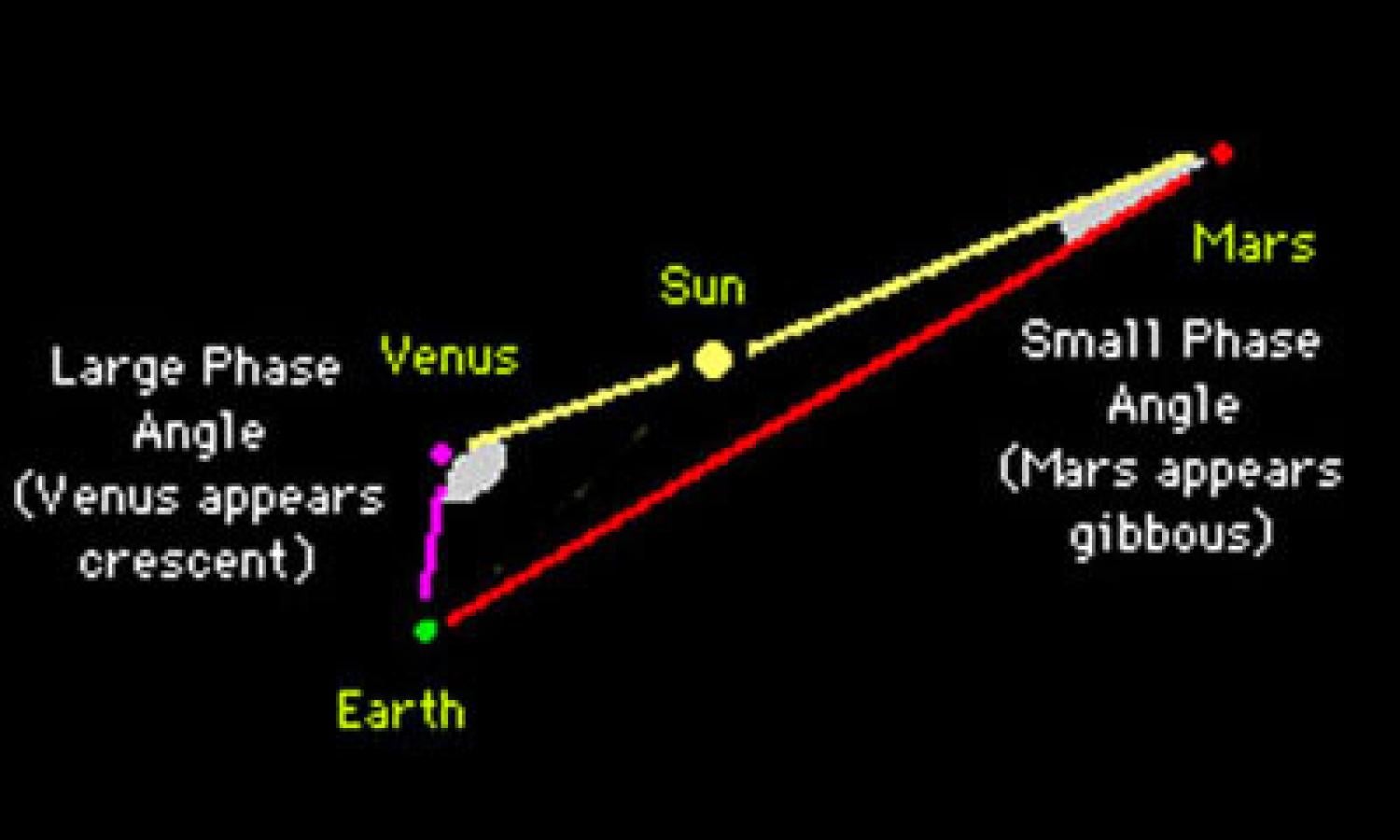
Phases Illumination diagram
From the viewpoint of the inferior planets (Mercury and Venus), the angle between the Sun and Earth can vary all the way from 0 to 180 degrees - so, back on the Earth, we can (at least theoretically) see the illumination of these planets change from 100% to 0%. Of course, we can't actually observe these two extremes, since in these cases the planet is in either superior or inferior conjunction with the Sun, and is lost in its glare. Typically, we can observe inferior planet phases ranging between about 90% down to about 10% illumination.
From a distant, outer (superior) planet's viewpoint, the Earth is always huddled close to the direction of the Sun - so the phase angle is always small, and the percent illumination of that planet, as seen from Earth, is always very nearly 100%. That's one reason why the Voyager spacecraft's flyby images of Saturn were so spectacular - for the first time ever, we saw Saturn and its rings with side-illumination.
Magnitudes (Apparent Brightness)
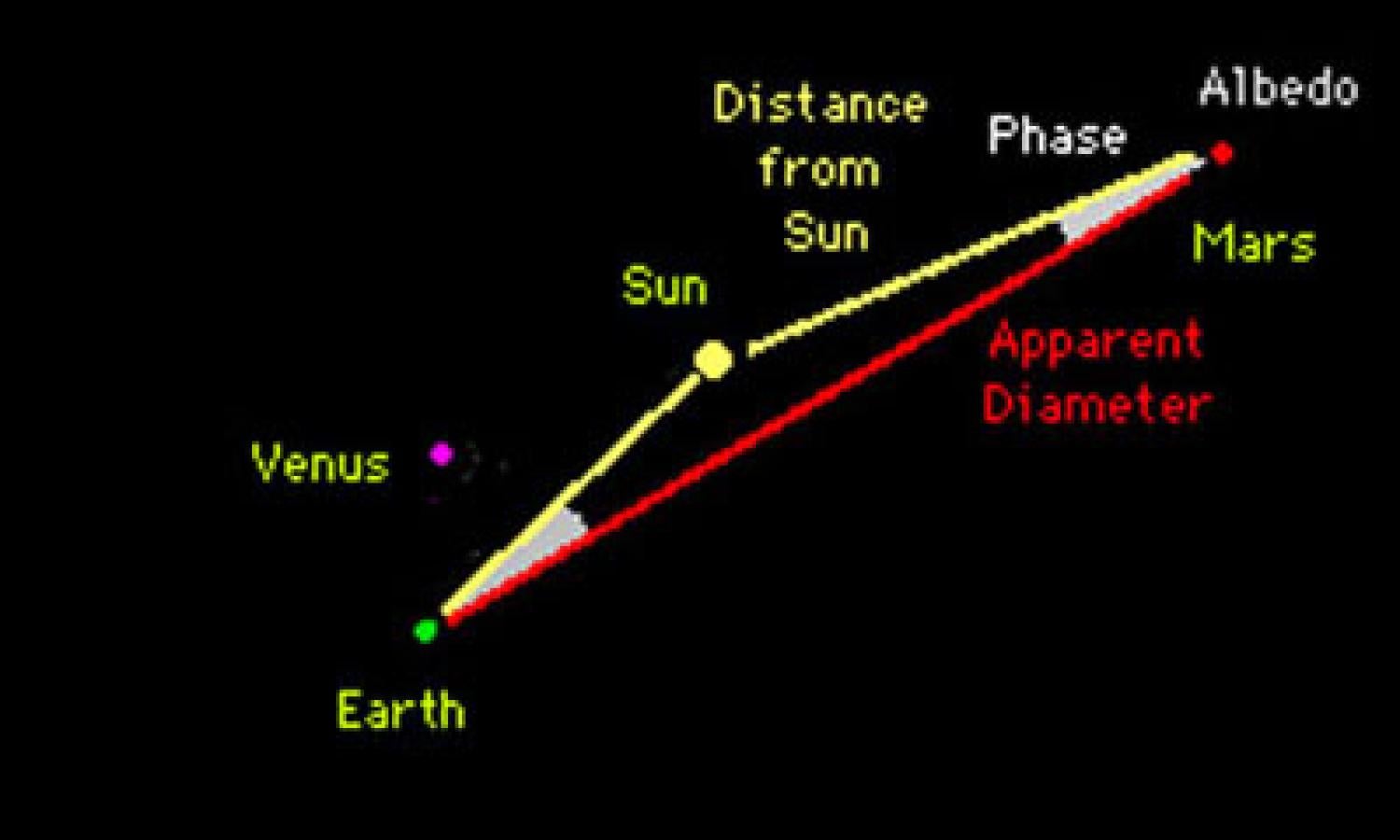
Magnitudes diagram
One magnitude unit means a difference of 2.512 times in brightness. Two magnitudes represents a brightness difference of 2.512 x 2.512 = 6.31. These odd numbers was chosen so that a difference of exactly 5 magnitudes is equivalent to a difference of exactly 100 in brightness (or 2.5 magnitudes is a brightness difference of exactly 10). Now you know just how strange astronomers are ...
The apparent brightness of a planet depends upon a number of factors. First, you have to figure out the apparent diameter of the planet's disk, as seen from Earth (discussed above). Next, you have to account for what fraction of that disk is illuminated (also above). Putting the two together, you can figure our how much area of the sky is filled with light from the planet.
But planets shine by reflected sunlight, so you also have to figure in its albedo - the reflectivity of the planet averaged out over its entire surface. And finally, you have to figure out just how strong the sunlight is when it reaches the planet, before reflection. That can be quite a big factor, since the intensity of sunlight falls off as the square of its distance from the Sun.
All of this, put together, shows us why Venus is always so bright in the sky (around magnitude -4): Venus is only 0.7 AU from the Sun, so it receives twice as much sunlight as does the Earth (and 50 times more than Jupiter, 5 AU from the Sun). And it comes close to us, so that its angular diameter can become quite large. And finally, its albedo is quite high, meaning that it is very reflective. The only factor that diminishes its brightness is the fact that we only see a portion of its illuminated face. Oddly enough, Venus' orbit is such that, as its apparent diameter grows larger when nearing the Earth, its phase shrinks by almost exactly the same amount - so that the total illuminated angular area remains unchanged. Hence the magnitude of Venus is virtually constant, regardless of whether its phase is a fat gibbous or a thin crescent!


