Visualizing Number Theory Spring 2017

- to develop methods of visualizing Gaussian prime numbers
- to develop software for computer experimentation with abelian sandpiles associated to the Gaussian Schmidt arrangement
Supervising:
- Dr. Eric Stade
- Dr. Katherine Stange
Students:
- Sharon Huh
- Paul-Robert Laliberte
- Chloe Pradeau
- Jack Werner
Gaussian Primes
In the integers, a prime number is one which has no proper factors (i.e. besides +/- 1 and +/- itself). The Gaussian integers are the complex numbers a+bi where a and b are integers. These integers also have unique factorization and a notion of prime, i.e. one which is divisible only by units (1,-1,i,-i) and associates of itself (itself times a unit). Examples include 1+i and 2+i, but not 3+i=(1-i)(1+2i).
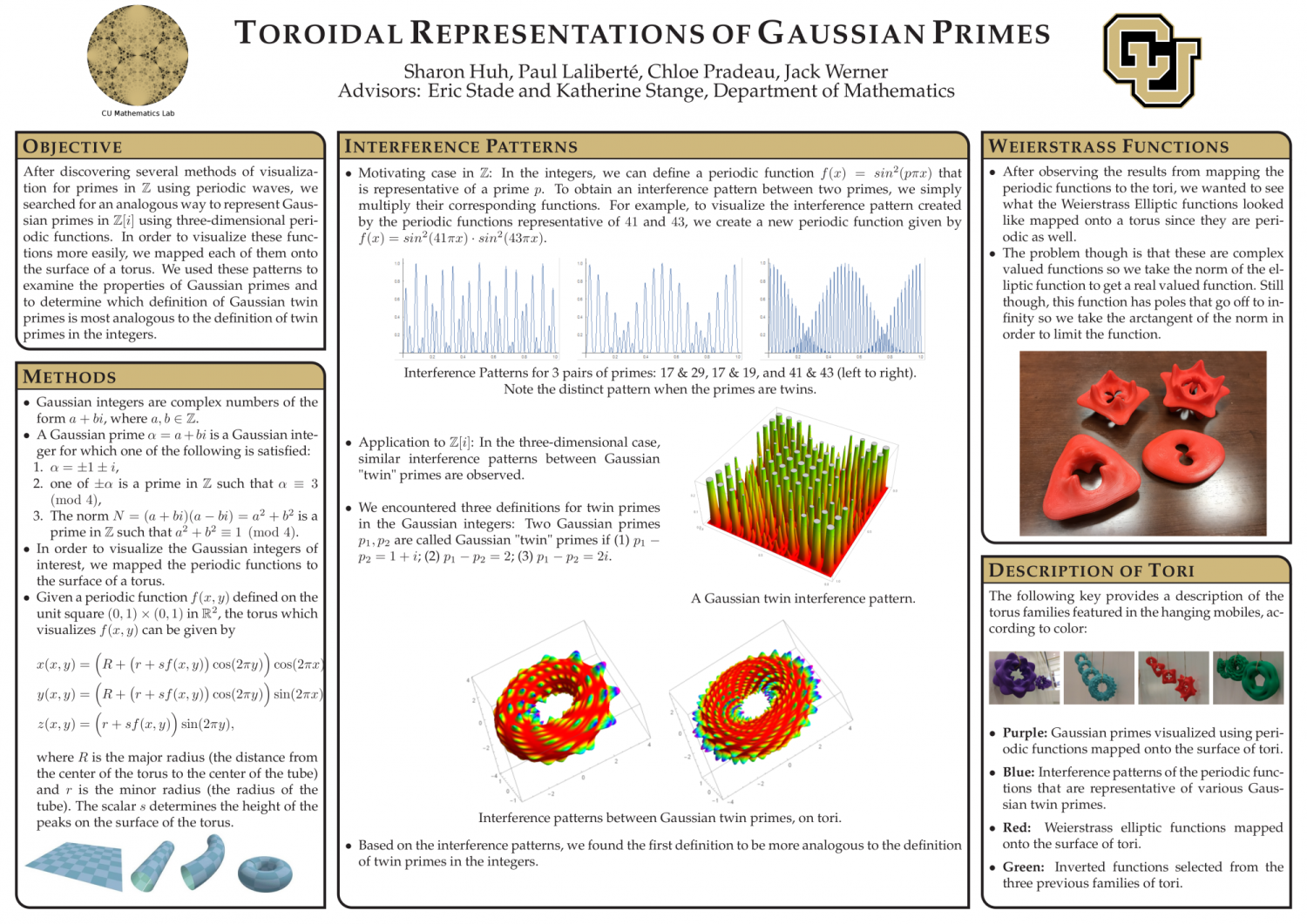
The students investigated a variety of ways to explore such integers and primes, including notions of twin primes. Students settled on a central tool, which was to associate to an integer or prime a doubly periodic function on the complex plane. To each prime (or integer) is associated a lattice inside the Gaussian integers, formed of all multiples of that integer. When points on the plane are considered modulo this lattice, one obtains a torus. In analogy to a periodic sine wave of a given frequency, the students created periodic functions periodic with respect to the lattice. They then investigated a variety of ways to graph these functions on the torus, as 3d printed models.
The team created a series of 3d printed tori the size of doughnuts, illustrating various families of double-periodic functions with certain periodicities. Here we are at work:

These have been on display at Gemmill Engineering, Math & Physics Library since Summer 2017, along with an explanatory poster (click on the picture below for a full version):
If you would like access to the resulting 3d printer files, please use this links:
- Compressed zip of STL files to print tori (these print bagel halves which must then be glued together)



Gaussian Sandpile Software
An abelian sandpile is a dynamic arrangement of 'chips' on the vertices of a finite graph. Beginning with some starting distribution of chips, one allows a vertex to 'fire' if it has more chips than it has neighbours, sending one chip to each neighbour. If one continues this process, the arrangement may stabilize, meaning there are no more vertices with enough chips to fire; or it may be recurrent, repeating a pattern over and over.
A recent paper of Levine, Pegden and Smart describes a series of stable configurations of chips on a regular square lattice. As it turns out, these configurations are periodic with respect to various sublattices. They can be parametrized, quite surprisingly, by the circles in an Apollonian circle packing. An Apollonian circle packing is a fractal arrangement of tangent circles pictured here:

This packing is just a part of a larger picture called the Gaussian Schmidt Arrangement, shown here:

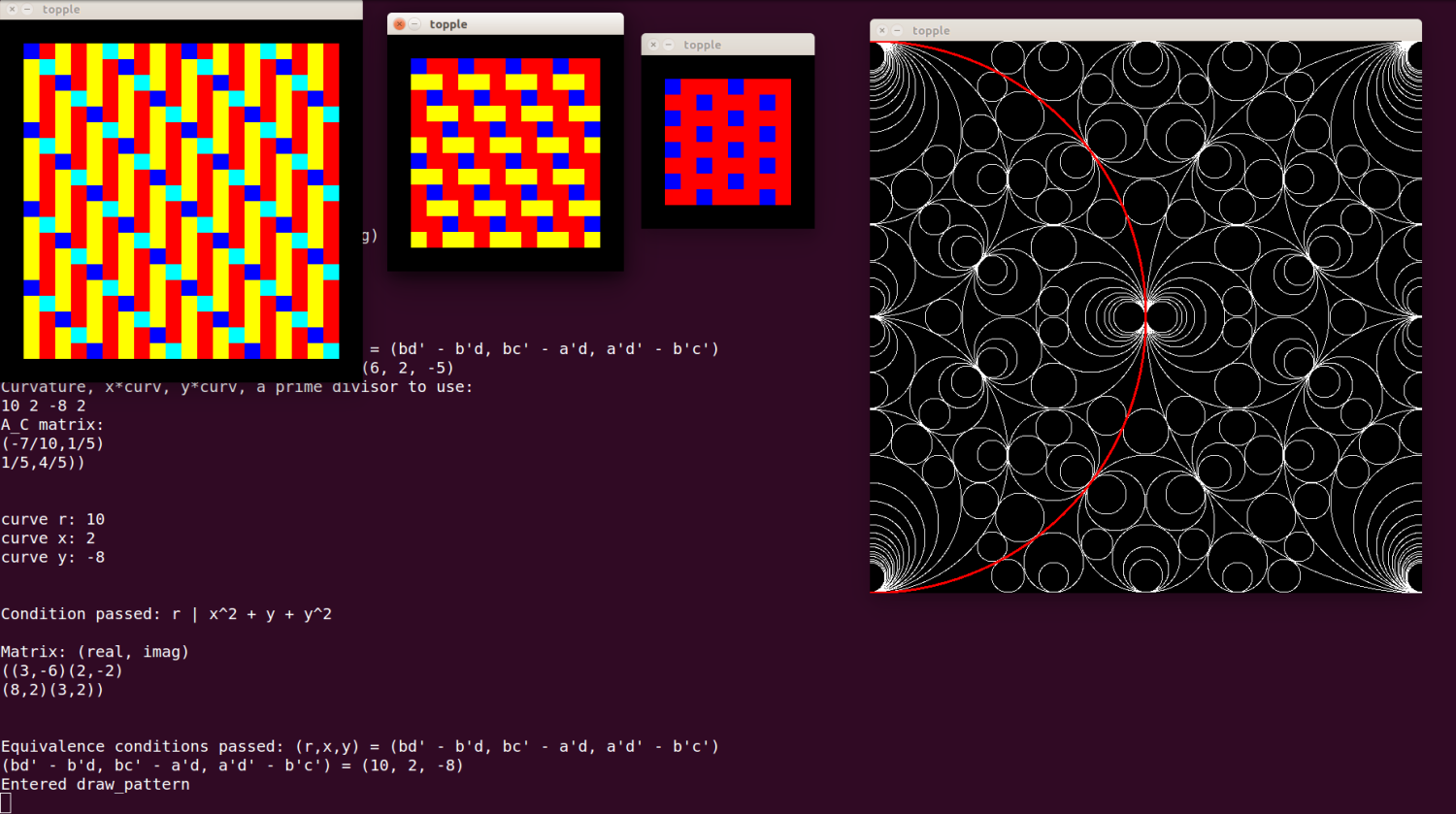
In fact, each circle in the Gaussian Schmidt Arrangement also has an associated sandpile. Students programmed software to create the sandpile associated to each circle, so the researcher can interact with the data with a graphical user interface. They used an algorithm due to graduate student Daniel Martin.
Shown here is a screenshot of the resulting software.
If you would like access to the software, please visit github:
Back to the Experimental Mathematics Lab