Supervisor: Dr. Camilo Mesa
Description:
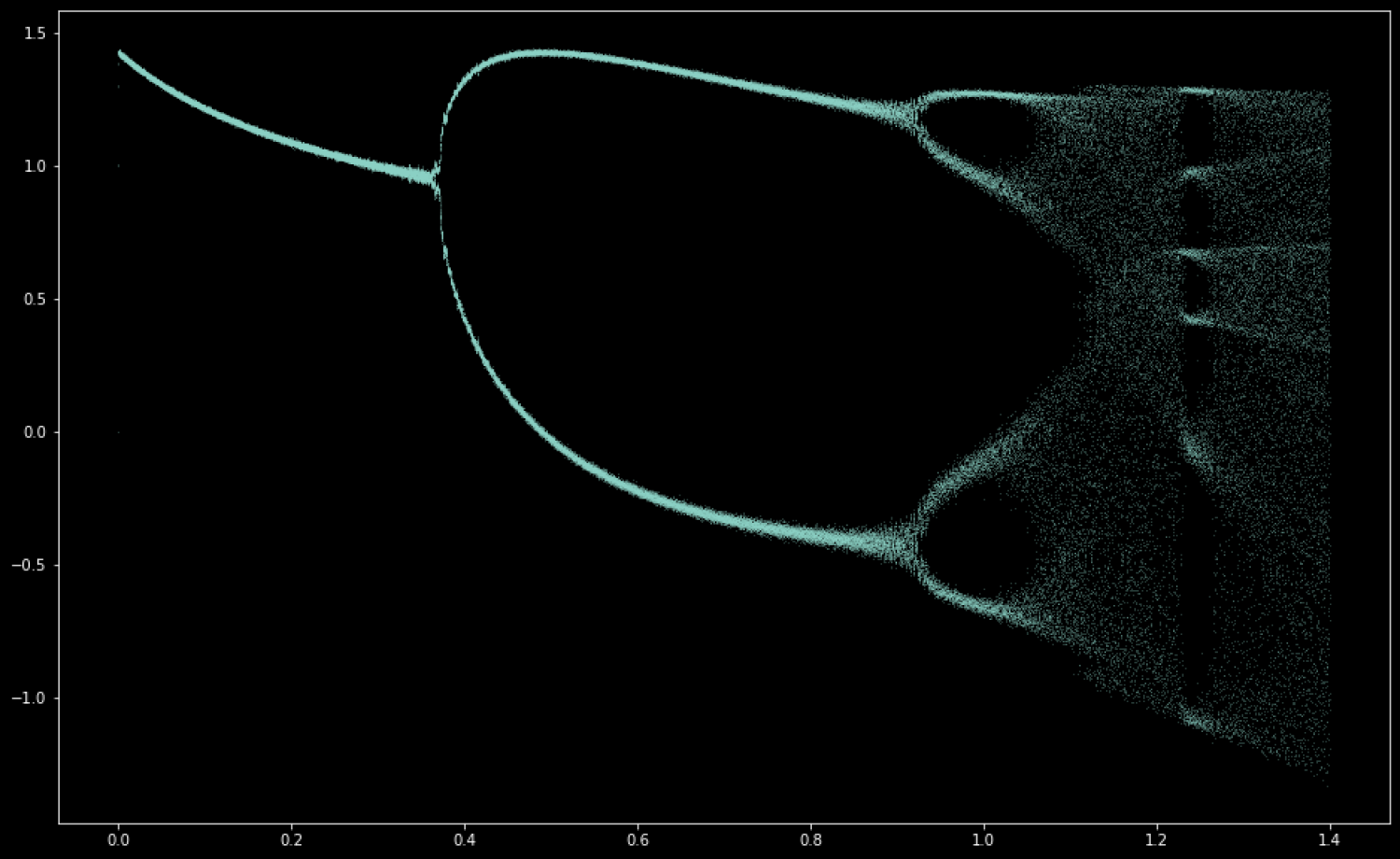
Topological data analysis (TDA) is a methodology designed to study qualitative properties (shapes) of data using topological, statistical, and computational ideas. This topological framework has provided new insights when exploring multi-dimensional and noisy data sets such as gene expression from breast tumors, image processing, signal, and time-series analysis (Nature, Sci Rep 3, 1236 (2013)). One of the tools of TDA, called Mapper, is based on the idea of partial clustering of the data guided by a set of functions defined on the data. Mapper reduces high-dimensional data sets to a graph with nodes corresponding to clusters in the data, which can be visualized. Other methods of TDA are based on Persistence Homology, which quantifies shapes in data (components, loops, flares, cavities, etc.) that persist through different resolutions. In particular, TDA can help detect and quantify periodic patterns in data and regime changes in chaotic dynamical systems using time series analysis. Our investigation will be example-based and will explore various possible applications in science and industry. Each participating student will choose a data set that can be analyzed using these tools and their programming and aim to conjecture new patterns and insights.
Students:
Diego Delgado Alvarez
Bao Bui Thien Nguyen
Andrew Scheck
Back to the Experimental Mathematics Lab.