Numberscope (Fall 2022)

Team:  3-6 students

Supervisors:  Dr. Katherine Stange, Dr. Glen Whitney (Studio Infinity) and Liam Mulhall

Students:  Olivia Brobin, Devlin Costello, Clyde Kertzer, Jenny Leong

Description:

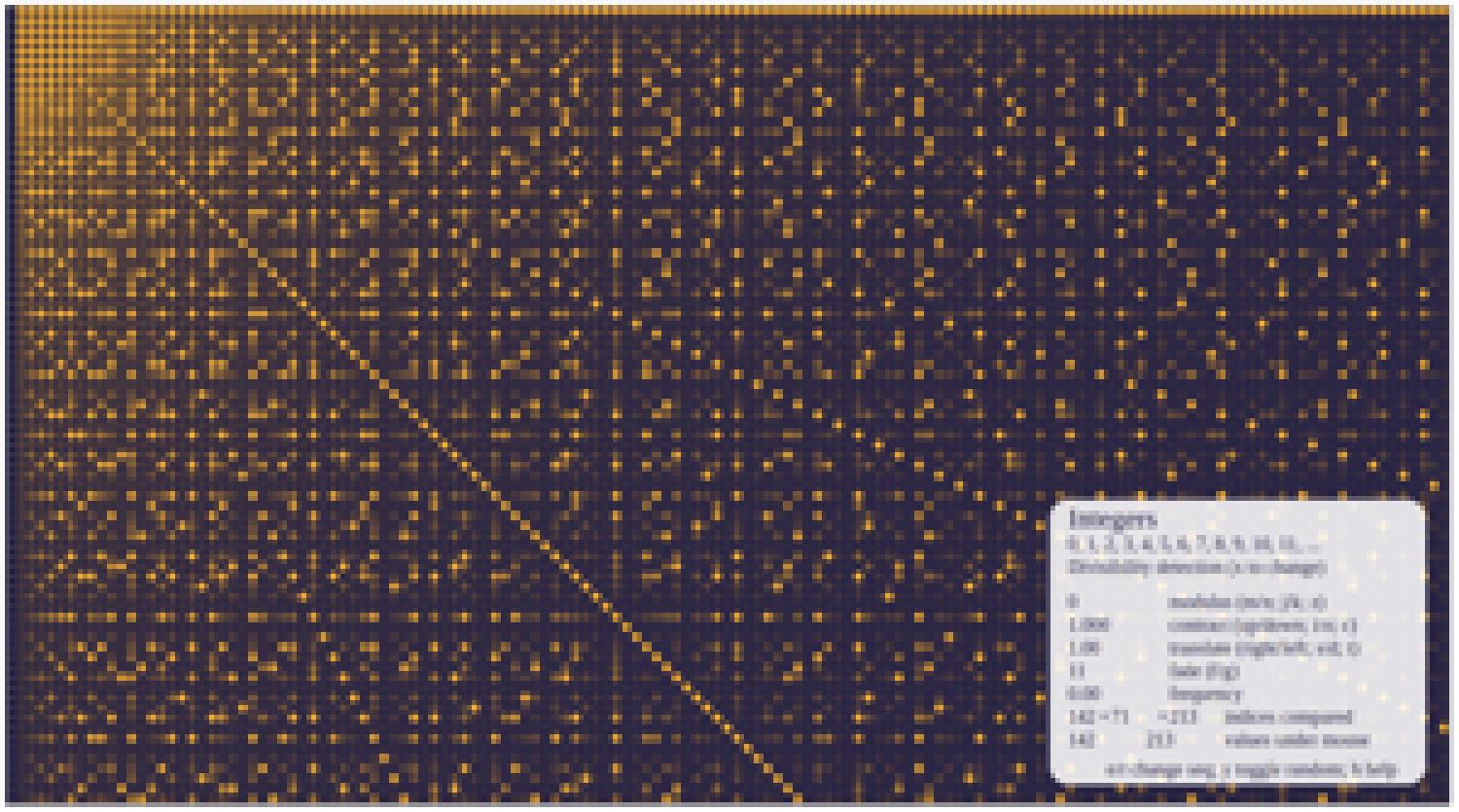
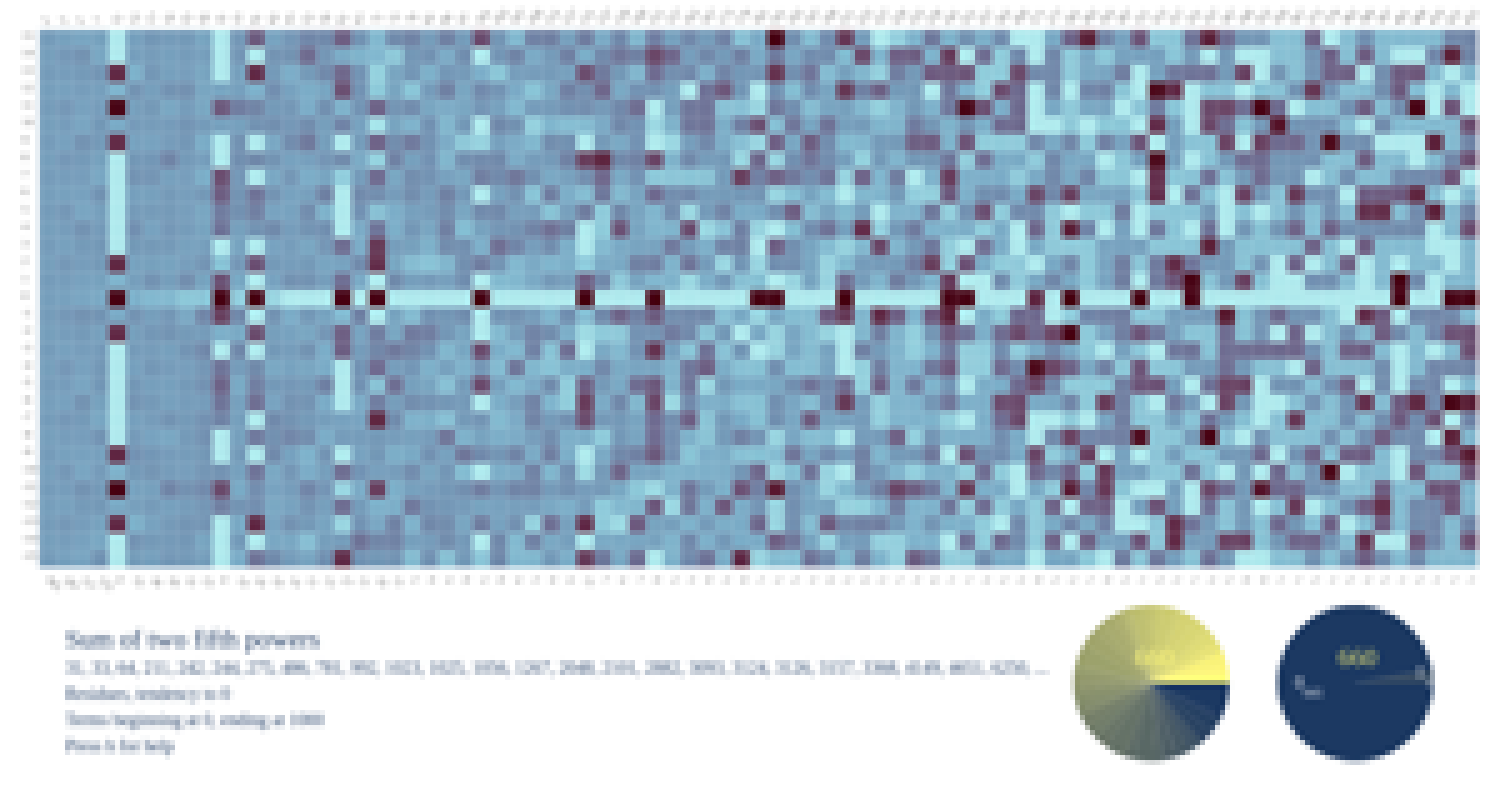
Numberscope is an online tool, designed for researchers, hobbyists and artists, to visualize integer sequences.  Integer sequences arise in all areas of mathematics and science, and they can have all sorts of interesting properties:  factorization properties, statistical properties, even fractal self-similarity.  These properties lend themselves to visualization.  In Numberscope, one can combine a favourite integer sequence (say, chosen from the On-Line Encyclopedia of Integer Sequences), with ready-made interactive visualization tools. 

The Numberscope platform is currently under development (GitHub), and the team will serve two primary purposes:  (1) to explore mathematics through computer illustration and experimentation, and (2) to provide user experience on the tool and to help improve it.  Each student will develop their own visualizer to incorporate into numberscope, written in TypeScript (a type-annotated version of JavaScript, the most common language for front-end web programming).  Students can further explore mathematical questions with their new tool, or work on the graphic design or software development of the tool itself.

Students will be expected to have mathematical curiosity, together with experience programming in at least one language.  Students who do not know TypeScript should be independent enough to learn it on the go.  Students with some software development experience or web graphics design experience (and/or an eagerness to learn these skills) will be welcome to participate in the development of the web software itself.

Outcomes:

Students each made their own visualizers!  View progress on the GitHub.  

Jenny Leong:

In this visualizer, the brightness of each circle represents how quickly the inverse of a
number in the sequence, raised to the power of n, approaches zero as n increases.
Each prime number is assigned a color which corresponds to the number's prime
factors. This color-coding scheme allows you to see which prime factors are
associated with each number in the sequence.
For example: Here are circles representing 2,3,4,5,6.

The 1st and 3rd circles (2 and 4) have the color orange, which represents their prime
factor – 2.
The right-most circle’s color is a combination of 2’s color and 3’s color since 2 and 3
are the prime factors of 6.
Also, the brightness of each circle shows how quickly the inverse of the
corresponding number approaches zero when raised to the power of n. For example,
the 2’s circle is “blurrier” than the 6’s circle because 1/(6)^n approaches zero faster
than 1/(2)^n when increasing n.
By looking at the colors and brightness of the circles, you can gain insight into the
behavior of the numbers in the sequence as n increases.
Use the left arrow key to show/hide the color label of prime factors.
Use the right arrow key to show/hide the label of each circle.
Use the "[" key to increase the overall brightness of circles.
Use the "]" key to decrease the overall brightness of circles.

Back to the Experimental Mathematics Lab.