Supervisor: Dr. Tianyuan Xu and graduate student Sarah Salmon

Students:

  • Saurabh Totey
  • Natalie Schoenhals
  • Wei Qu

Project Website:  https://math.colorado.edu/~tixu6187/mathlab.html

Project Description:

Consider the set Sn of all rearrangments of the numbers 1,2,3,...,n.  We may represent each rearrangement in Sn by diagrams like the ones below, where we use oriented strings to indicate where each number ends up. 

 

Diagrams representing a permutation of {1,2,3,4,5}. The middle diagram decomposes the permutation into four "basic transpositions'' which only interchange two adjacent strings. The heap of the permutation can be extracted from third diagram, where each basic transposition occurs as "low'', or as "early'', as possible.

 

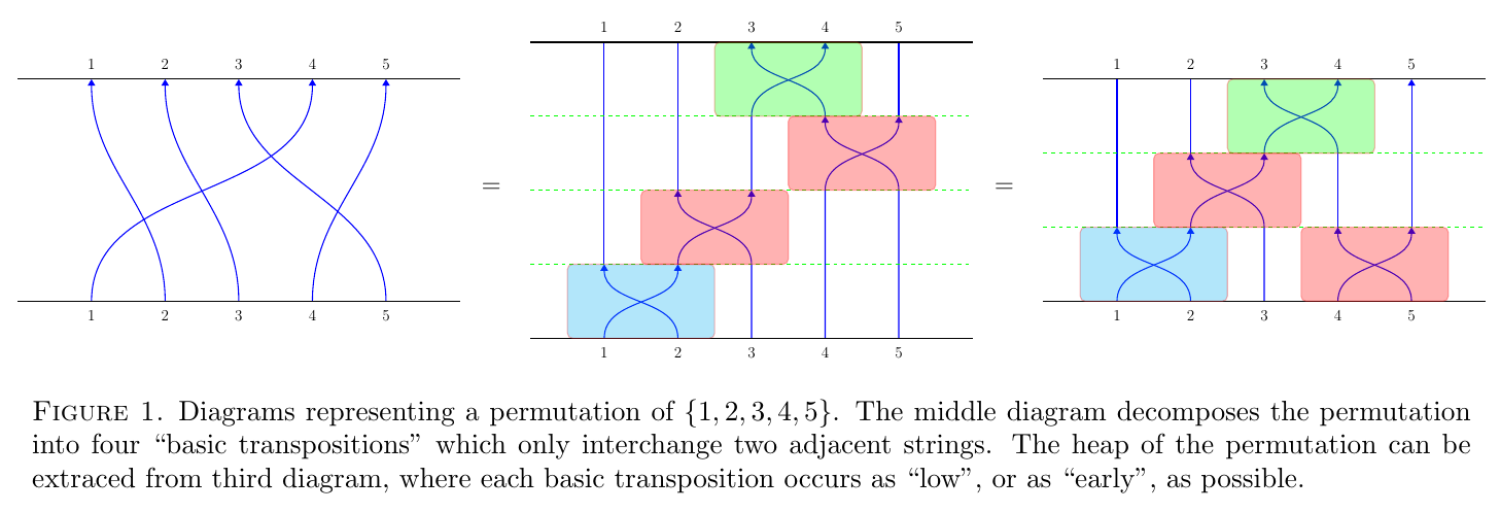
Doing so quickly reveals a number of interesting facts about Sn:

  1. First, we may identify each rearrangment with the function, or permutation, that takes the source of each string to its target. Moreover, we can compose these functions, just as we can stack the diagrams.
  2. Second, once we "pull some strings'', we realize that all the diagrams can be obtained by stacking diagrams which only swap two adjacent strings, therefore all the permutations can be obtained by composing those functions which only swap two adjacent numbers. 
  3. Third, we see that some pairs of crossings in a diagram can slide past each other while some cannot. This explains why we are able to push the higher red box  in the second picture to the bottom level to get the third picture, but we cannot slide the green box past any red box. It turns out the configuration of the boxes in the third picture, with every boxed pushed as low as possible, forms an interesting object called a heap.

The above story about Sn has an interesting generalization: the set Sn is known as a symmetric group and admits a generalization to Coxeter groups, structures with rich connections to a field of mathematics called representation theory. Furthermore, Coxeter groups and the heaps of their elements are closely related to both theretical physics and computer science. In particular, they are related to the so-called Temperley--Lieb algebras from statistical mechanics  and to the so-called trace monoids from the theory of concurrent computation.

The goal of this project is to implement and study heaps of Coxeter group elements in the computer algebra system SageMath. A large number of mathematicians use SageMath to aid their research, and a successful implementation of heaps could contribute to current, active research in representation theory.

 

Project Summary:

Using symmetric groups as guiding examples, we started the project by learning the basic properties of Coxeter
groups, fully commutative (FC) elements of Coxeter groups, and heaps of FC elements. We then learned the basic
functionalities of SageMath and started the implementation of FC elements in SageMath. We completed two programs.
One of them can test efficiently whether a given element in a Coxeter group is FC or not; the other program can
recursively generate all FC elements of a given Coxeter group up to any specified Coxeter length. In an effort to
optimize our code, we studied the implementation of recursive functions, breath-first search algorithms, and
depth-first search algorithms in SageMath in detail.

The programs we wrote are helpful for the computation of objects attached to FC elements arising from
Kazhdan--Lusztig theory, such as so-called generalized Temperley--Lieb algebras and Kazhdan--Lusztig cells.
Moreover, both the code and the ideas developed during our project became foundations of another undergraduate
research project that Tianyuan led and Natalie again participated in. In particular, the programs we wrote were
supplemented to a module on FC elements that is now officially incorporated into SageMath; documentation for the
module can be found at https://doc.sagemath.org/html/en/reference/combinat/sage/combinat/fully_commutative_elements.html.

 

Return to the Experimental Mathematics Lab.