Quantum Monte Carlo

There are two flavors of QMC, (a) variational Monte Carlo (VMC) and (b) projector Monte Carlo (PMC). VMC starts by proposing a functional form for the wavefunction and then optimizes the parameters of the wavefunction to minmize the energy. At the end of the minimization one obtains a state that has the largest overlap with the ground state of the system, subject to the constraints imposed by the chosen functional form. In PMC one simply performs a imaginary time propagation which is akin to numerically cooling the system down to 0 K. At the end of this process one obtains the ground state energy and wavefunctions. PMC is exact in principle, however, while performing imaginary time propagation one has to use stochastic methods and these suffer from a fundamental problem known as the sign problem. The sign problem typically limits the accuracy with which accurate results can be obtained. In our work we work on both VMC and PMC, in the particular the flavor of PMC that we work on is known as auxiliary field quantum Monte Carlo (AFQMC). We briefly describe the recent developments in AFQMC that have originated from the work done in my group.

Auxiliary field quantum Monte Carlo (AFQMC)

AFQMC is a variant of PMC, and the algorithm is used to stochastically sample Feynman paths in the Hilbert space of the system (see the figure). Although it was invented in the late 1970s, the formulation suitable for quantum chemistry only emerged about two decades ago, in 2003. Since then, this method has been adopted by about a dozen research groups, and several tens of articles have appeared in the last few years. One study from the Reichman group conducted a benchmark study of AFQMC to compare its accuracy with that of CCSD(T). Unfortunately, the results showed that, for virtually all benchmarks, AFQMC is less accurate than CCSD(T). Additionally, AFQMC has two additional shortcomings: (a) it is more expensive than CCSD(T), and (b) obtaining properties other than ground state energies, such as excited states or dipole moments, which are routine with equation of motion CC, is not easy to achieve using AFQMC. In the last few years, we have addressed each of these three shortcomings,
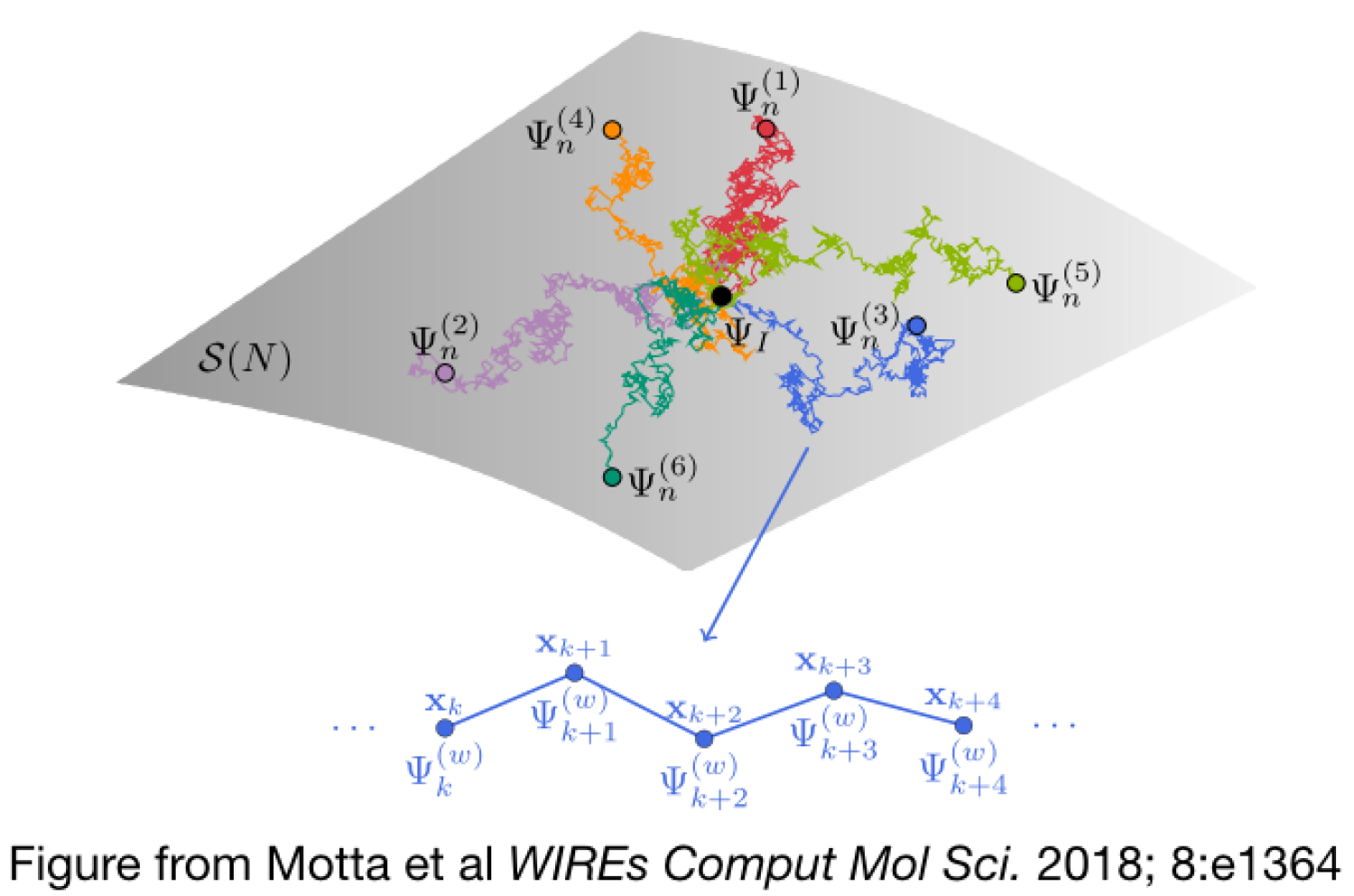
as outlined below.

(a) Accuracy of AFQMC:

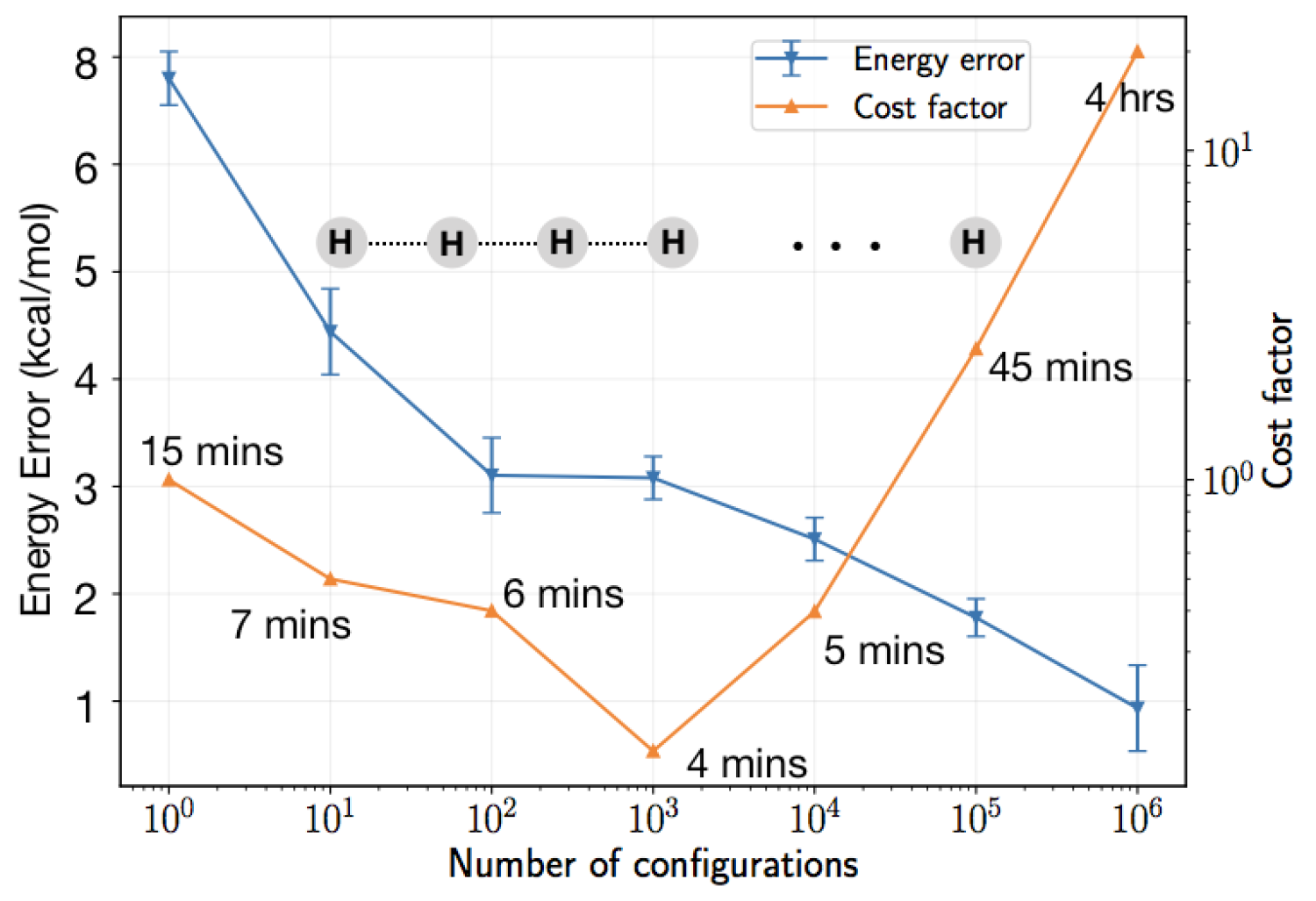
AFQMC can be seen as a method that takes information about the system and a trial state as input and provides the stochastic realization of the ground state and its energy as output. The only uncontrolled approximation made in AFQMC is the phaseless approximation, which relies on the quality of the trial state. In the impractical scenario where the trial state is the exact state, AFQMC yields exact results. However, in practice, a single determinant, such as the Hartree-Fock or DFT wavefunction, is typically used as the trial state. When attempting to enhance the accuracy of the trial state by including a larger number of determinants (N_d determinants), the calculation cost typically increases linearly with the number of determinants (shifting the cost from O(N⁴) to O(N_dN⁴)), restricting the trial state to only about 100 determinants. To overcome this limitation, my group has developed a novel algorithm that reduces the scaling to O(N_dN +N⁴) instead of O(N_dN). This represents a significant improvement in CPU cost and qualitatively alters the types of problems that can be tackled with AFQMC. For instance, as shown in the Figure, for a hydrogen chain increasing the quality of the trial state not only improves the accuracy of AFQMC but remarkably achieves this higher accuracy at a lower computational cost. This is facilitated by the fact that as the quality of the trial state improves, the noise in the simulation decreases. Additionally, because the cost of including a larger number of determinants is relatively inexpensive, higher accuracy can be achieved at a lower cost. Our algorithm has already been taken up by other groups. It was recently used by the Friesner group to investigate a large benchmark comprising more than 300 molecules, including those in the G2, G3, and W4 datasets, predominantly featuring weakly correlated molecules where CCSD(T) exhibits extremely high accuracy. When AFQMC was used with a multiSlater trial employing our algorithm, utilizing fewer than 10,000 determinants (with a computational cost roughly equivalent to AFQMC with a single Slater trial state), the errors were reduced to below those of CCSD(T). This represents one of the first systematic studies involving a large benchmark of weakly correlated molecules where a method has been competitive with CCSD(T), excluding composite methods that themselves rely on CCSD(T) to capture the majority of the correlation energy.

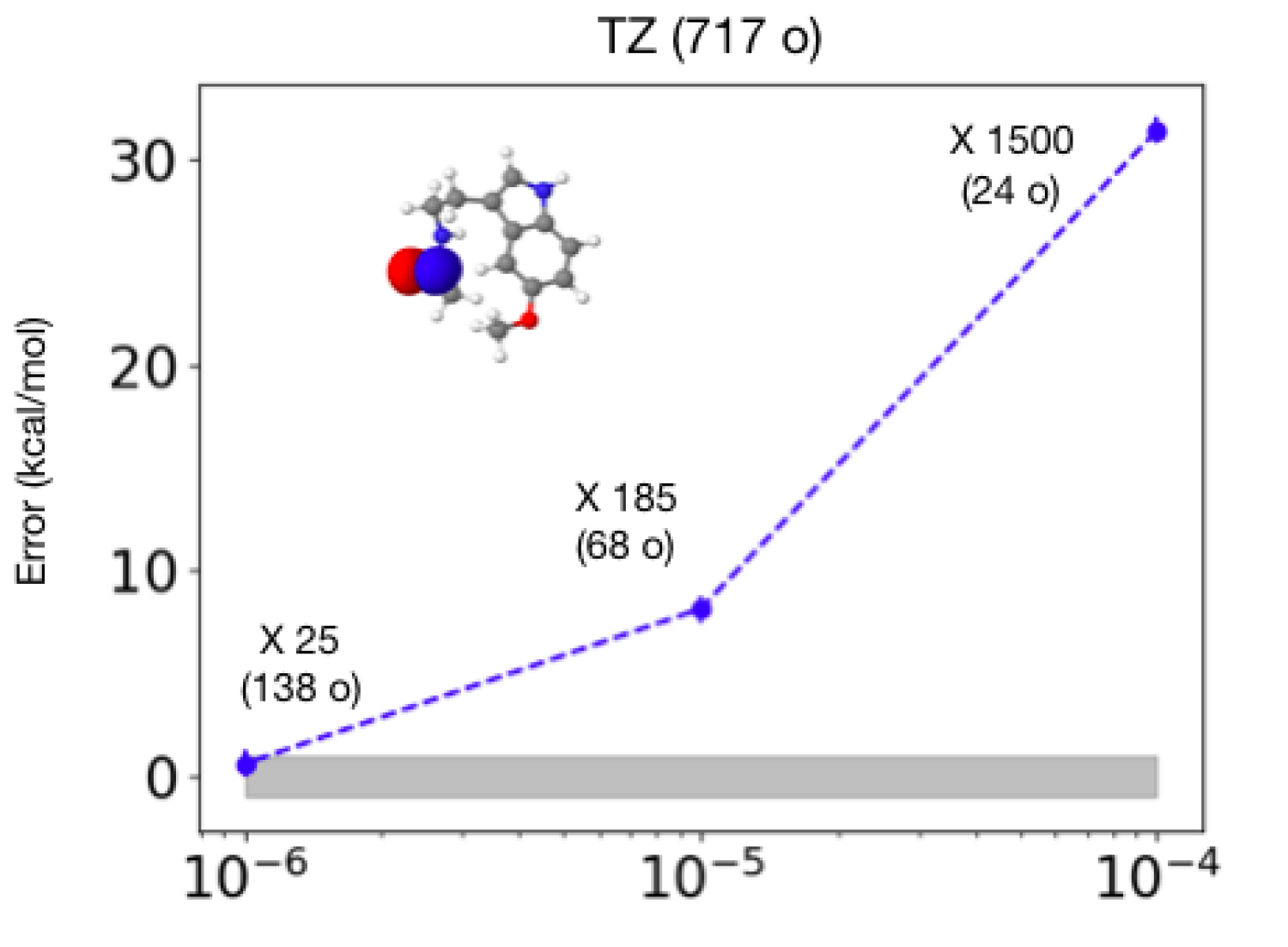
(b) Linear and sub-linear scaling AFQMC: 

 The computational cost of AFQMC grows as the fourth power of the size of the system, more precisely, it grows as the third power for a constant multiplicative error and as the fifth power for a constant additive error. However, recent advancements in the area of local correlation theories underscore that this scaling is unphysical. For sufficiently large system sizes, it should be possible to achieve a linear scaling algorithm. We employed the local natural orbital (LNO) formulation to develop a linear scaling AFQMC algorithm, which proves to be more efficient than canonical AFQMC even for relatively small systems such as metalonin, containing only 90 valence electrons and 700 orbitals with a triple-zeta basis. The figure on the left shows that as we tighten the relevant thresholds for linear scaling the accuracy increases and with the tighter thresholds we get chemical accuracy with x25 speedup. In fact, our algorithm outperforms linear scaling deterministic algorithms when one is interested in a given multiplicative error (e.g., error per electron) because its cost is independent of the size of the system (a similar sub-scaling stochastic algorithm for DFT has been developed by Rabani, Baer and Neuhauser). For example, if we want to determine which of the two phases of a disordered system has a lower energy, this question can be answered with a CPU cost independent of the system's size. This marks a significant improvement over linear scaling CCSD(T) and broadens the scope of AFQMC to address several problems that are either impossible or very difficult to answer using even linear scaling CCSD(T). 

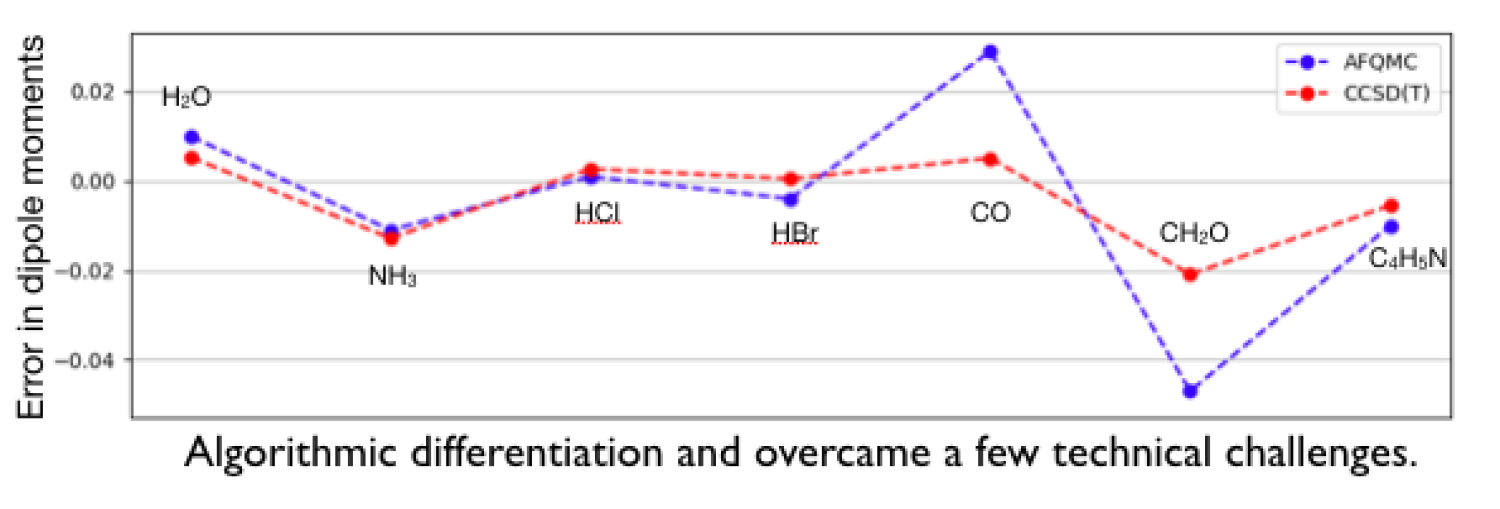
(c) Properties using AFMQC: 

A long-standing challenge for AFQMC, as with most other projector Monte Carlo algorithms, including diffusion Monte Carlo (DMC), is the inability to obtain properties at the same level of accuracy as the electronic energy. This limitation stems from the fact that these methods provide only a stochastic realization of the wavefunction. Recently, we overcame this drawback by employing linear response theory, which operates on the same principles as experiments and many other quantum chemistry methods, including EOM-CC. To obtain response properties, we utilized the extensive theoretical work that originated in the machine learning community, allowing us to perform algorithmic differentiation of AFQMC without modifying the underlying method. To the best of my knowledge, this is the first time that linear response theory has been successfully used to obtain properties, not just for AFQMC but for any projector Monte Carlo method. The figure on the right shows that one can now get dipole moments with fairly high accuracy. The results can be improved if we used AFQMC with a multiSlater trail state. Work along this direction is ongoing.