When DFT or CC fails, then multireference methods are often the methods of choice in chemistry. In these methods one uses the “diagonalize-then-perturb” strategy, whereby the Hamiltonian is first diagonalized within a subspace of nearly degenerate orbitals known as the active space to capture what is commonly known as strong or static correlation. This is followed by perturbative correction to account for election correlation (commonly known as weak or dynamic correlation) from the remaining inactive orbitals. Multireference methods have been around for more than four decades now and for the most part are limited to small active spaces (< 16 orbitals) which in turn limits their accuracy. This is because of the limits that both steps of the method place on the number of active space orbitals, the cost of diagonalizing scales exponentially with the number of active space orbitals and the cost of performing the perturbation theory scales at least as the eighth power of the number of orbitals. To make progress one has to make improvements to both these steps and I will describe my group's work towards improving each of the two steps below.
Static Correlation using HCI
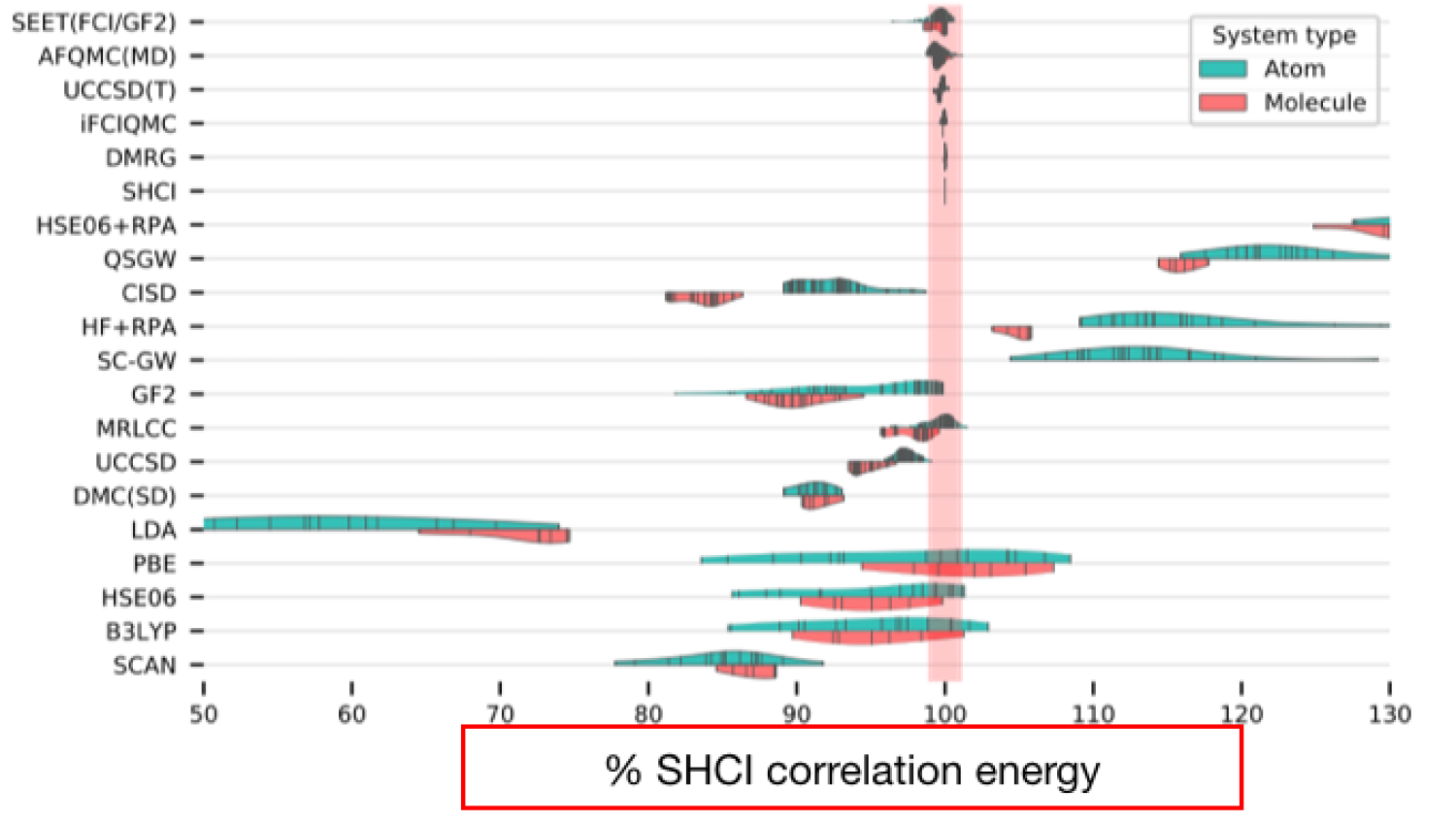
The very first algorithm that my group worked on is called the semistochastic heat bath configuration interaction (SHCI) and it is a particularly efficient flavor of the selected configuration interaction method. It allows one to obtain near-exact energies in active spaces containing hundreds of orbitals at a cost that is often orders of magnitude lower than competing methods. Our efforts in this area (along with that of others) has led to a recent revival of interest and an explosion of activity in the area of selected configuration interaction methods. In the context of SHCI my group has introduced the ability to perform (a) stochastic calculations to evaluate the perturbative corrections, (b) calculations with relativistic Hamiltonian, (c) calculate excited state energies, and (d) optimize orbitals allowing one to perform complete active space self consistent field theory (CASSCF) calculations. We have used SHCI to address several problems that have posed challenges for multireference methods including calculation of the; qualitatively correct triplet-quintet gap in the Fe-porphyrin, dissociation curves of Cr 2 with an accuracy and error bar that is significantly lower than previous methods, potential energy surfaces of organic molecules such as ozone and methylene in the gas phase. Finally, it was one of the most accurate methods in a large benchmark study for calculation of dissociation/ionization energies of transition metal oxides. This study was sponsored by Simon's institute and more than 10 researchers participated using various methods, some of which have been around for several decade. It was found that HCI was most accurate and in fact was used as a benchmark against which all other methods were benchmarked (in the figure the x-axis are the results obtained from HCI).
Dynamic Correlation using perturbation theory
Although treating active space
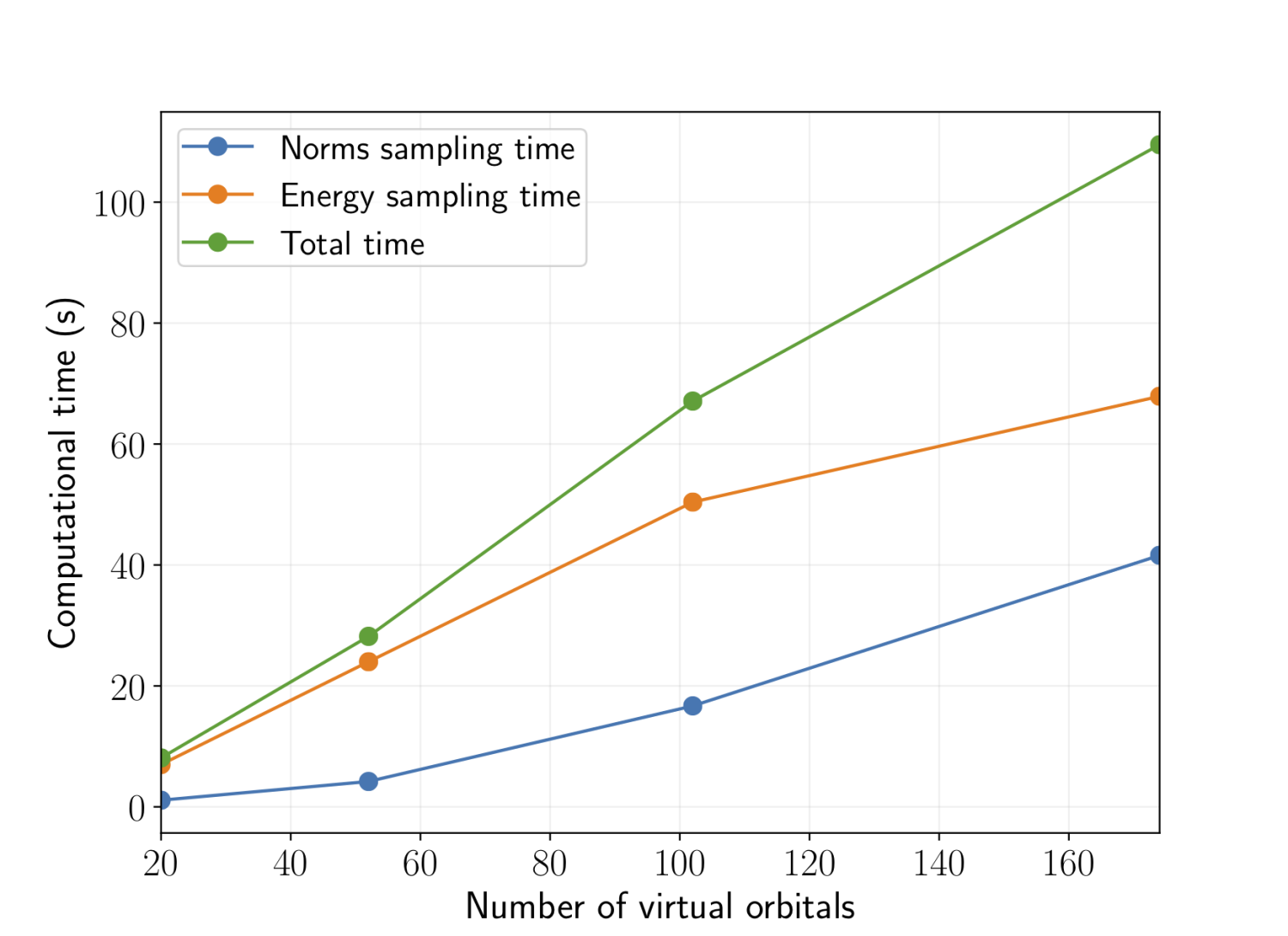
exactly gives us a wavefunction that is qualitatively correct, one still needs to include the dynamic correlation which accounts for the fact that there is a correlation hole around each electron. The reason for the difficulty in calculating dynamic correlation lies in the fact that most multireference theories require one to store up to fourth-order reduced density matrices (RDM), which becomes untenable for large active spaces. Recently, we have introduced a novel algorithm for performing a flavor of multireference perturbation theory known as NEVPT2 to correct wavefunctions with arbitrarily large active spaces. This was made possible by eliminating the need for storing these high order RDMs, which allows us to overcome the memory bottleneck. As a side benefit, the new algorithm also enjoys a lower prefactor and scaling with the size of the active and virtual space. The graph shows that the method scales close to linearly with the number of virtual orbitals.