Parametric versus Semi/nonparametric Regression Models
Course Topics
Linear models, generalized linear models, and nonlinear models are examples of parametric regression models because we know the function that describes the relationship between the response and explanatory variables. In many situations, that relationship is not known. The primary goal of this short course is to guide researchers who need to incorporate unknown, flexible, and nonlinear relationships between variables into their regression analyses.
Nonparametric regression differs from parametric regression in that the shape of the functional relationships between the response (dependent) and the explanatory (independent) variables are not predetermined but can be adjusted to capture unusual or unexpected features of the data. When the relationship between the response and explanatory variables is known, parametric regression models should be used. If the relationship is unknown and nonlinear, nonparametric regression models should be used. In case we know the relationship between the response and part of explanatory variables and do not know the relationship between the response and the other part of explanatory variables we use semiparmetric regression models. Any application area that uses regression analysis can potentially benefit from semi/nonparametric regression. R software will be used in this course.
This course covers:
- Differences between parametric and semi/nonparametric regression models.
- How do I know if I should use nonparametric regression model for my data?
- A comparison between parametric and nonparametric regression in terms of fitting and prediction criteria.
- Methods of fitting semi/nonparametric regression models.
Data sets:
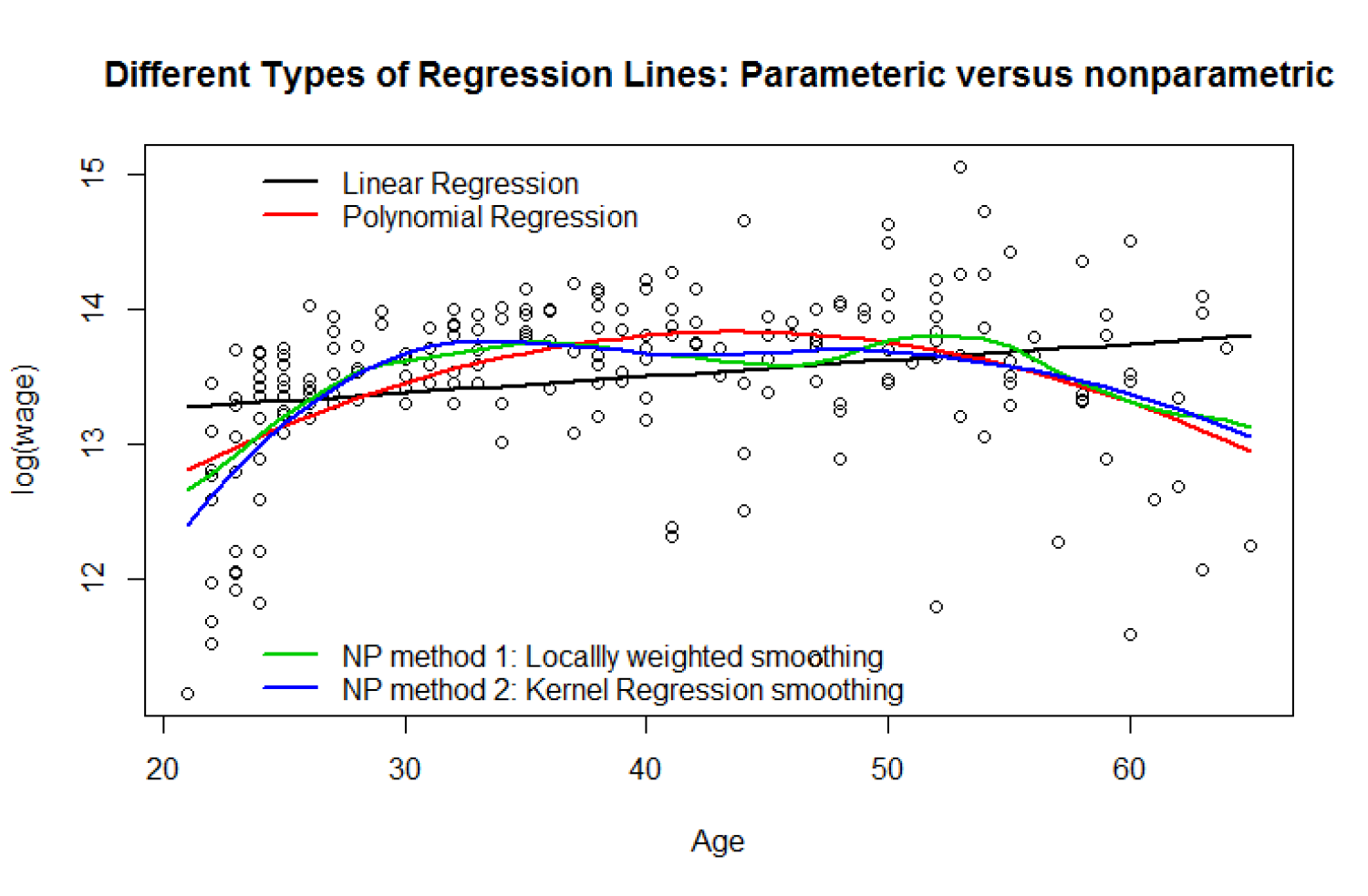
- We begin with a classic dataset taken from Pagan and Ullah (1999, p. 155) who considerCanadian cross-section wage data consisting of a random sample taken from the 1971 Canadian Census Public Use Tapes for males having common education (Grade 13).There are n = 205 observations in total, and 2 variables, the logarithm of the individual’s wage (logwage) and their age (age). It is available in R software package.
- Prestige of Canadian Occupations data set. This data have 6 variables: education, income, women, prestige, census, and type. Source: Canada (1971) Census of Canada. Vol. 3, Part 6. Statistics Canada [pp. 19-1–19-21]. It is also available in R.
- Cross-sectional wage data are consisting of a random sample taken from the U.S. population survey for the year 1076. There are 526 observations in total. Available in R software [library(np), data(wage1)]
Below is an example for unknown nonlinear relationship between age and log wage and some different types of parametric and nonparametric regression lines. One can see that nonparametric regressions outperform parametric regressions in fitting the relationship between the two variables and the simple linear regression is the worst. We are going to cover these methods and more.
[video:https://vimeo.com/102770660]
LISA Short Course: Parametric versus Semi/nonparametric Regression Models from LISA on Vimeo.

