Research
Current photovoltaic devices have a limit on how much energy can be collected from sunlight: photons with insufficient energy are not absorbed and photons with excess energy create excitons that thermalize before being collected. One way to increase this limit would be to convert the high-energy photons into more than one exciton each.
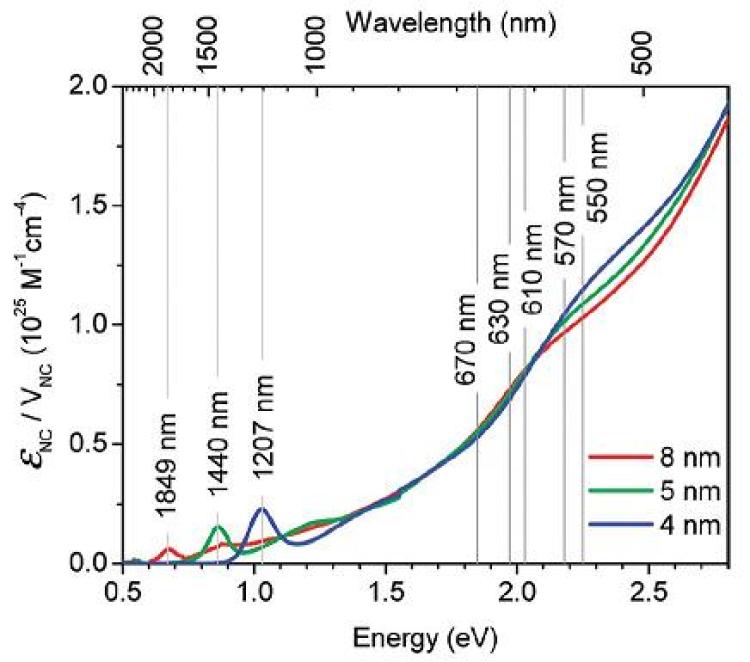
There is experimental evidence that multiple exciton generation can happen in semiconductor quantum dots, but the mechanism is unclear. A semiconductor quantum dot has a size large compared to lattice constants but small or comparable to the bulk Bohr exciton radius. In this situation, an excited electron is delocalized with respect to its parent atom but confined to the quantum dot. The same is true for the empty orbital left behind, which is called a hole. The electron and the hole together are termed an exciton.
When forming an exciton by optical excitation, any photon energy above the band gap, Eg, is distributed between the hole and the electron. This excess energy puts the electron and hole far from thermal equilibrium with the crystal, and potentially even with each other. The cooling of these "hot" carriers can occur by a variety of methods. Two methods of interest in quantum dot multiple exciton generation theories are phonon emission and impact ionization. In phonon emission, an exciton excites a vibration and scatters as a lower-energy exciton. In impact ionization an electron or hole loses excess energy by exciting another electron into the conduction band, thereby creating another exciton. Studies in the Jonas group include a variety of nonlinear spectroscopies in order to measure the timescales and importance of these mechanisms.
Students Involved: Jisu, Alina, Alexa, Callum
Spectral interferometry measures time delays and spectral phase shifts between ultrafast pulses in two mutually coherent beams of light from the frequency domain power spectrum of the superposed beams. Applications of spectral interferometry include pulse characterization, optical component characterization, surface profiling, and optical coherence tomography. Active stabilization of a Mach-Zehnder interferometer is achieved through a feedback loop that maintains a balance of CW laser intensity between two interferometer outputs by employing a PZT attached to one arm's retroreflector. We are working to automate the computer control of the entire setup to maintain this active stabilization at desired pulse time delays for various time-resolved spectroscopic measurements.
Accurate spectral interferometry does require the restoration of the incident spectrum from the measured spectrum using the effective linespread function (incorporating line broadening, shift, and sampling effects of the spectrograph) and frequency calibration of the spectrometer and pixelated detector. Using our method, we restore interferograms using experimentally recovered asymmetric and varying effective linespread functions. The standard Fourier Transform Spectral Interferometry algorithm then is able to retrieve the spectral phase difference and time delays to match the experimental stability, limited only by Fourier filtering of charge coupled devices and interferometer imperfections. The constant phase shift and slope delay accuracies achieved will now enable more accurate line shapes in future 2D spectroscopy experiments.
Students Involved: Jisu, Alina, and Callum
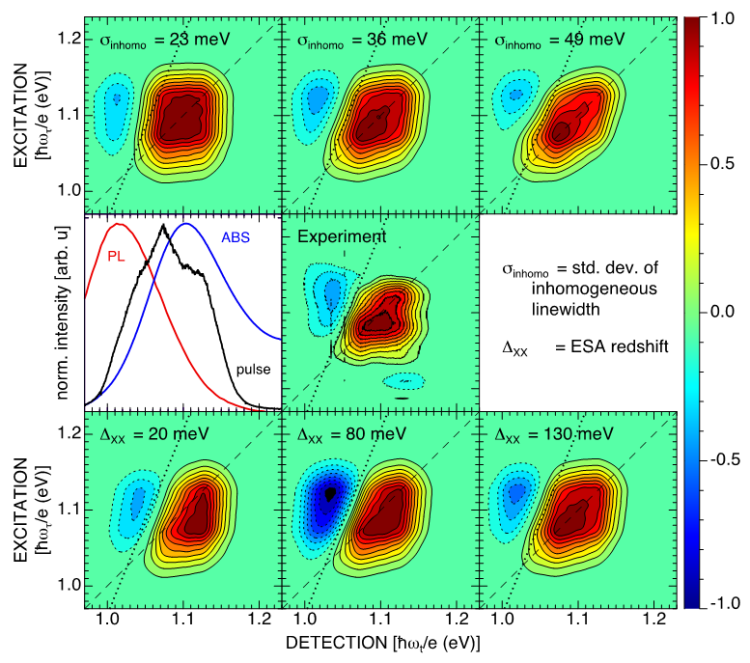
Multidimensional spectroscopy is an increasingly common tool for physical chemists. Optical analogs of the NMR COSY and NOESY experiments have now been performed. These measurements are more susceptible to artifacts and distortion than their one-dimensional counterparts. The differences between optical and NMP spectroscopy make it difficult to detect and quantify distortion.
The Jonas group has focused on understanding and/or eliminating distortions of 2D optical spectra. Once understood, these findings can easily be generalized to further understanding of one-dimensional signals and their distortions as well. Distortions considered are due to absorption of the sample, beam crossing geometry and spectrometer/detector imperfections. Knowledge of distortions and their corrections will enable the study of even weak couplings between strong or widely separated optical transitions. Such couplings are thought to be important for an understanding of photosynthesis, solar energy conversion, and conical intersection dynamics.
Further development of tunable ultrashort visible and near-infrared pulses from noncollinear optical parametric amplifiers as well as continued instrumentation work to improve interferometric pulse time delay accuracy and interferometric signal detection accuracy should lead to more accurate 2D spectra.
Students Involved: Jisu, Alexa, Alina, Callum
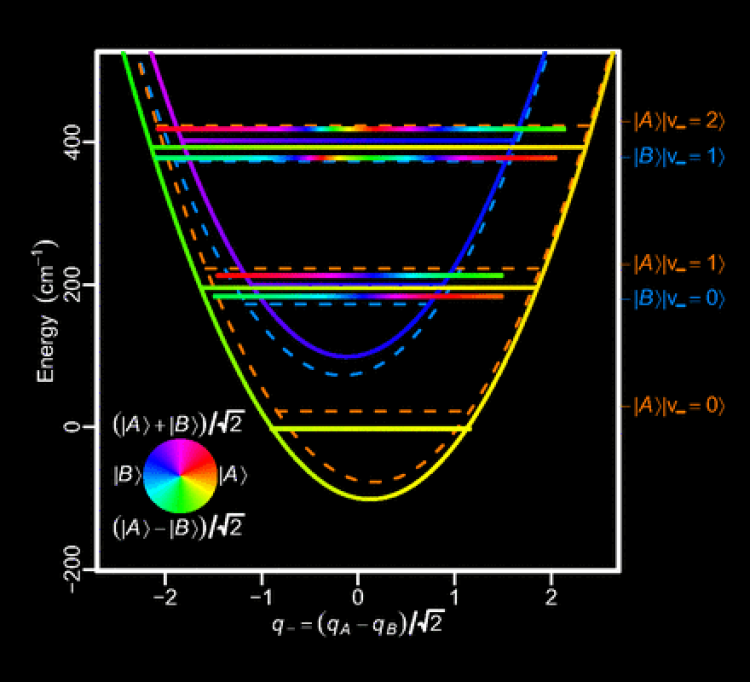
Efficient energy transfer between photosynthetic molecules can be accurately calculated using nonadiabatic dynamics at locations of vibronic resonance when potential energy surfaces of excited states differ by only a vibrational quantum. Based on the work published in PNAS in 2013 by Tiwari, Peters, and Jonas, our group continues to explore vibronic resonances and their effect on nonadiabatic dynamics, expanding our theoretical model to examine more complicated systems.
We also look to use the model of the photosynthetic energy transfer to calculate ideal parameters for the synthesis of nanomaterials that can take advantage of resonant energy transfer to optimize efficiency.
Students Involved: Peter
For most systems, it is fair to assume that electronic and vibrational motion occur on different timescales and can be factored using the adiabatic approximation. However, in some systems (which include but are not limited to conical intersections) adiabatic potential energy surfaces do not properly describe the dynamics and an exact nonadiabatic factorization as described by Hunter is more helpful in accurately describing the dynamics.
This factorization describes the wavefunction using an amplitude and an electronic character at each point. This accurately describes the total probability distribution and scattering type experiments that correspond to it. An interesting phenomenon occurs, however, when a finite number of electronic states contribute significantly as the probability amplitude can be zero. Where this occurs, there arise nodes with a general conical shape.
At points of high symmetry, such as at the point of a circularly symmetric conical intersection, there may or may not be nodes and these nodes can have higher order character. Our group studies systems like these to more fully understand these nodes and how they contribute to our understanding of nonadiabatic dynamics.
Students Involved: Peter


