Direct Numerical Solutions to Stochastic Differential Equations with Multiplicative Noise

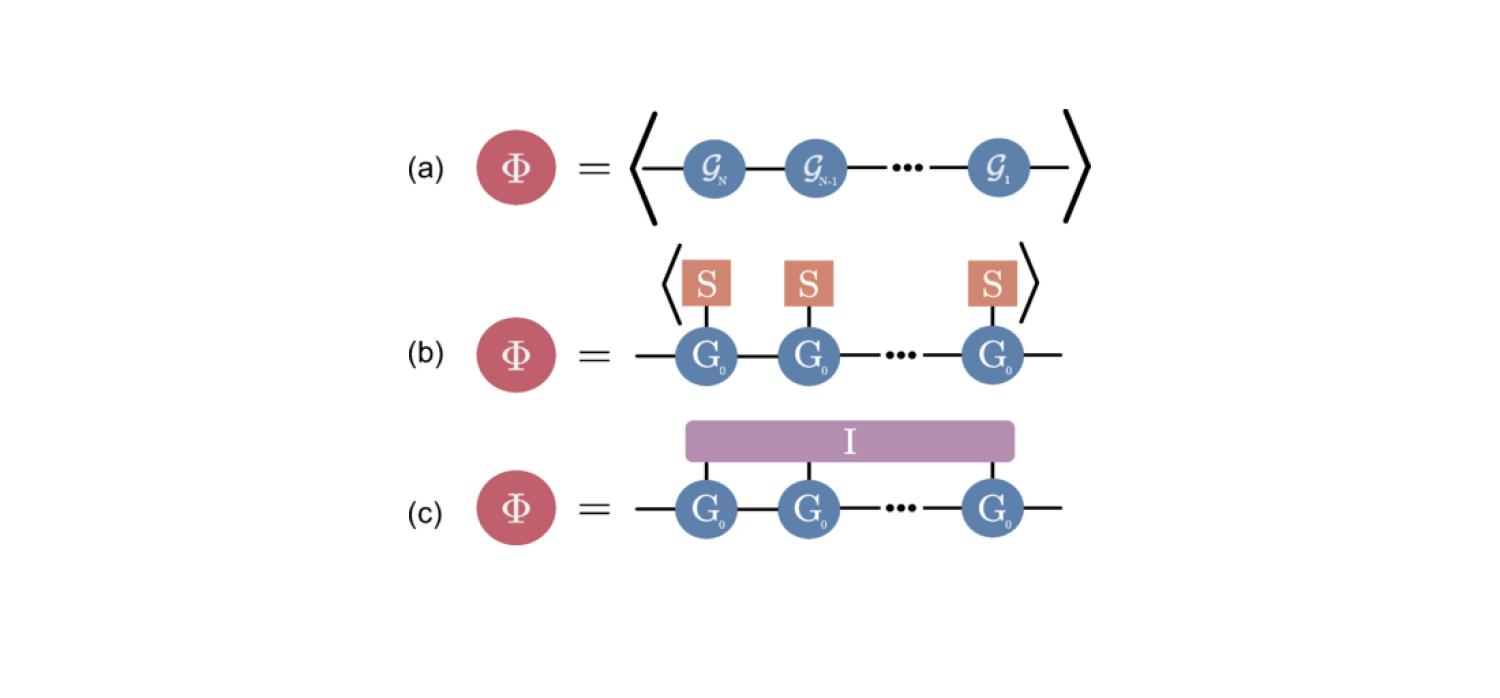
Inspired by path integral solutions to the quantum relaxation problem, we develop a numerical method to solve classical stochastic differential equations with multiplicative noise that avoids averaging over trajectories. To test the method, we simulate the dynamics of a classical oscillator multiplicatively coupled to non-Markovian noise. When accelerated using tensor factorization techniques, it accurately estimates the transition into the bifurcation regime of the oscillator and outperforms trajectory-averaging simulations with a computational cost that is orders of magnitude lower.

Ryan T. Grimm and Joel D. Eaves Direct Numerical Solutions to Stochastic Differential Equations with Multiplicative Noise Phys. Rev. Lett. 132, 267101 (2024)