Effects of soft interactions and bound mobility on diffusion in crowded environments: a model of sticky and slippery obstacles
Michael W. Stefferson, Samantha A. Norris, Franck J. Vernerey, Meredith D. Betterton, and Loren E. Hough (2017). Physical Biology 14, 045008. DOI: 10.1088/1478-3975/aa7869. Download.
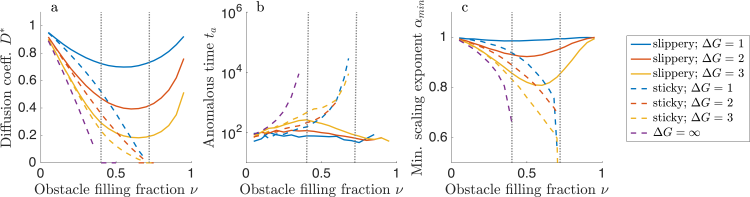
Crowded environments modify the diffusion of macromolecules, generally slowing their movement and inducing transient anomalous subdiffusion. The presence of obstacles also modifies the kinetics and equilibrium behavior of tracers. While previous theoretical studies of particle diffusion have typically assumed either impenetrable obstacles or binding interactions that immobilize the particle, in many cellular contexts bound particles remain mobile. Examples include membrane proteins or lipids with some entry and diffusion within lipid domains and proteins that can enter into membraneless organelles or compartments such as the nucleolus. Using a lattice model, we studied the diffusive movement of tracer particles which bind to soft obstacles, allowing tracers and obstacles to occupy the same lattice site. For sticky obstacles, bound tracer particles are immobile, while for slippery obstacles, bound tracers can hop without penalty to adjacent obstacles. In both models, binding significantly alters tracer motion. The type and degree of motion while bound is a key determinant of the tracer mobility: slippery obstacles can allow nearly unhindered diffusion, even at high obstacle filling fraction. To mimic compartmentalization in a cell, we examined how obstacle size and a range of bound diffusion coefficients affect tracer dynamics. The behavior of the model is similar in two and three spatial dimensions. Our work has implications for protein movement and interactions within cells.

