hydrohalos

Deviations from hydrostatic equilibrium in the circumgalactic medium: spinning hot haloes and accelerating flows

Benjamin D. Oppenheimer¹
1 CASA, Department of Astrophysical and Planetary Sciences, University of Colorado, 389 UCB, Boulder, CO 80309, USA

Abstract

Hydrostatic equilibrium (HSE), where the thermal pressure gradient balances the force of gravity, is tested across a range of simulated EAGLE haloes from Milky Way L∗ haloes (M₂₀₀ ≈ 10¹²M_⊙) to cluster scales. Clusters (M₂₀₀ 10¹⁴M_⊙) reproduce previous results with thermal pressure responsible for ∼90% of the support against gravity, but this fraction drops for group-sized haloes (M₂₀₀ ≈ 10¹³M_⊙) and is even lower (40 − 70%) for L^∗ haloes between 0.1 − 0.3R₂₀₀. Energy from feedback grows relative to the binding energy of a halo toward lower mass resulting in greater deviations from HSE. Tangential motions comprise the largest deviation from HSE in L∗ haloes indicating that the hot circumgalactic medium (CGM) has significant sub-centrifugal rotation and angular momentum spin parameters 2 − 3× higher than the dark matter spin parameter. Thermal feedback can buoyantly rise to the outer CGM of M200 10¹²M_⊙ haloes, both moving baryons beyond R₂₀₀ and feeding uncorrelated tangential motions. The resulting hot halo density and rotation profiles show promising agreement with X-ray observations of the inner Milky Way halo, and we discuss future observational prospects to detect spinning hot haloes around other galaxies. Acceleration and radial streaming motions also comprise significant deviations from HSE, especially net outward accelerations seen in L∗ and group haloes indicating active feedback. Black hole feedback acts in a preventative manner during the later growth of group haloes, applying significant accelerations via shocks that do not feed tangential motions. We argue that HSE is a poor assumption for the CGM, especially in the inner regions, and rotating baryonic hot haloes are a critical consideration for analytic models of the CGM.

Python Code to Analyze Simulations and Produce Plots in this Paper 

Please e-mail Ben Oppenheimer (beop5934@colorado.edu) to obtain the code to analyze other simulations and produce the plots in this paper.  As of now, the code works on EAGLE Project simulations run with Gadget-3, and the galmanip library written by Oppenheimer can be adapted to other simulations.  

This Website

This website provides supplemental materials for this paper.  It allows further exploration of the hydrodynamic state of the circumgalactic medium (CGM) using these and other simulations that are not in the submitted paper.  It includes extra figures and several visualizations.  

Additional Description and Extra Figures

The decomposition of the Euler equation into component support terms (thermal pressure, tangential motions, streaming motions, and acceleration) balancing the gravitational force works surprisingly well for the CGM.  While this method has been used previously for the ICM, the multi-phase nature of the CGM and the greater importance of feedback make its use more difficult, but not prohibitively so for the CGM.  Also, this method is used to diagnose the dynamics of the CGM and to lead to a discussion about the implications of deviations from hydrostatic equilibrium (HSE), and it is not meant to account for every force at every location within the CGM.

Having said that, the support terms often add up to near unity, which is rather stunning given that a 1-dimensional spherical distribution that relies on primarily one phase of gas is assumed for a 3-dimensional halo with complex, multi-phase structures arising from the >13 Gyr of evolution from cosmological initial conditions.  The spherical coordinates are gridded with fine radial logarithmic spacing that was chosen to show detailed fluctuations at the cost of having some spurious values, especially if there is a massive satellite or departures from sphericity in the stellar distribution.  There are forces that are not accounted for, including feedback, which in particular can apply forces inside 30 kpc of the CGM, and artificial viscosity added to the SPH equation of motion around shocks that can act as an additional pressure. 

The fiducial test halo is one that is not even in the main paper, but proved that this method could work as we show here.  It is a halo so rare, you will not likely find it in the real Universe, because it is a 10¹³ M_⊙ halo with no black hole feedback that has X-ray properties that are far too luminous compared to observations.  This halo, shown below, has low dark matter spin and has had no major mergers for quite some time.  Our method clearly shows that this halo is mainly in HSE inside R₂₀₀, with acceleration as the next largest component, but this halo demonstrates that the sum of the support terms outward (in orange) closely matches the gravitational force inward. Both logarithmic and linear representations are shown.

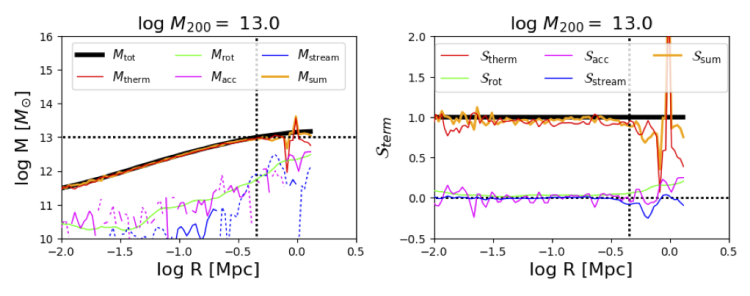
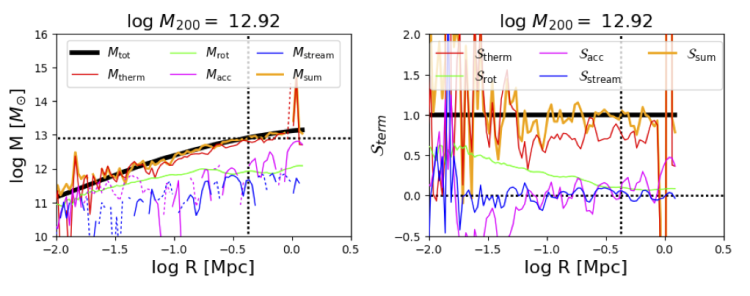
This NoAGN example spurred on the investigation of normal EAGLE halos that I had run as part of the exploration of the CGM with non-equilibrium effects (which are not important for the dynamics of these halos).  Below is the same halo with EAGLE feedback from stars and BHs.  I show these two examples in talks, and I worry that the EAGLE halo shows many ugly fluctuations that do not add up to one for every radial bin.   Yet the results are robust-- the inertial terms (rotation and radial streaming) increase and accelerations are larger and mirror the fluctuations in the thermal pressure gradient. 

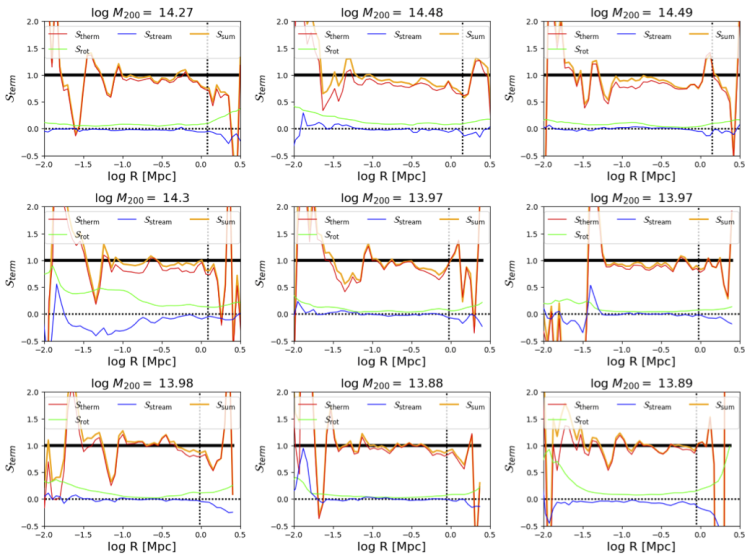
Medians and 25-75% spreads of the various support terms are shown in Figure 2 of the paper, because it shows nicely the general trends over samples of 9 halos each.  However, if you want to see the actual individual halos I include the here, and while they are not all perfect, they show some exciting variations and a lot of them do look quite good. Remember that I am plotting these on a linear scale (and traditionally cluster studies most often plot these on a logarithmic scale), so one can focus on the deviations.   For the L* halos, we pick the log(M₂₀₀)=12.28 halo, because it does look the best, however, I was surprised to see how well the halos at less that 10¹² M_⊙ looked, because these are definitely more multi-phase.  Surprisingly, the log(M₂₀₀)=12.23 halo looks the worse, and we used this in the 2016 O VI paper as the fiducial L* halo.  It has the most star formation and perhaps the most shocks in the inner 100 kpc of the CGM, so perhaps there are terms feedback and viscosity pressure that are not accounted for in our method.   It is rather stunning how universal the rotation term behavior is across all of these halos. 

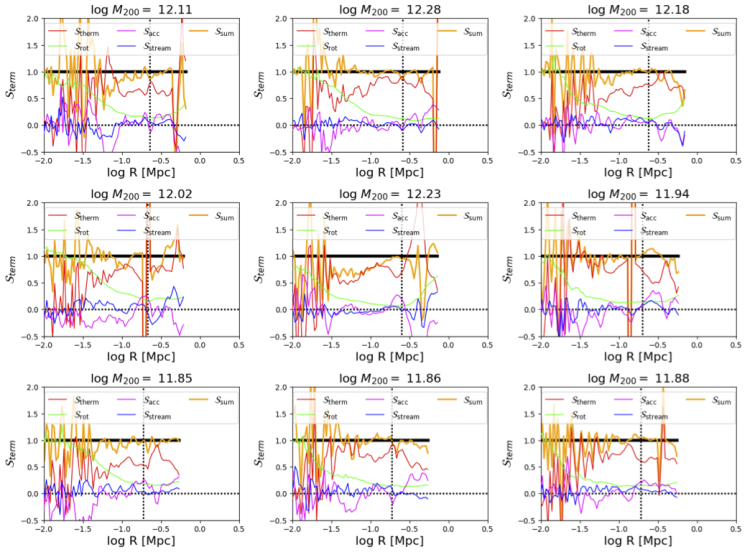
The group halos are also often quite messy indicating at least as significant of deviations in acceleration and streaming compared to the L* sample, despite being more thermally and less rotationally supported.  This may in part be due to more satellites with significant mass (even dominating the stellar mass budget in the >10¹³ M_⊙ halos), so a spherical assumption is not always a good case.  One surprise is how ubiquitous the acceleration term going negative at ~30 kpc, and whether this is related to shocks driven by AGN feedback preferentially showing up at this radius.    A lot of merging is going on in the log(M₂₀₀)=12.96 halo, and it is satisfying this halo’s terms add up to as close to one as they do.  The log(M₂₀₀)=13.16 halo was chosen to be merging, at z=0, so it probably is not as ideal to include in this exploration, but I did want to include the same 9 main halos for each L* and group sample that we have used throughout previous papers. 

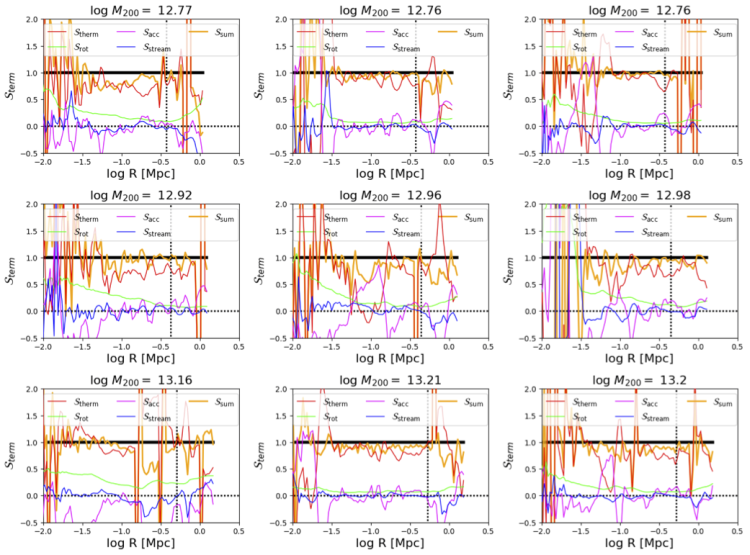
The “cluster” sample is from the EAGLE 100 Mpc box, and does not include the acceleration term, although it would certainly help to follow it to find the missing support.  I chose 9 of the 12 most massive halos that looked the best in these plots, because some of the most massive FOF groups tend to be unrelaxed since the largest scale power fluctuations preferentially sample late assembling halos.  The streaming terms (and likely the prospective acceleration terms that likely mirrors the thermal term) are smaller on average than the group halos, because an individual satellite cannot make such a large disruption to the overall dynamical balance of the halo. 

This method decomposing support terms of the CGM could be helpful for understanding the dynamics of various individual simulated halos.   Hopefully other simulation groups find this useful and can apply this to their halos.   Outputting acceleration, and even better breaking it down into various components (gravitational vs. hydrodynamical), is highly recommended.  There are many interesting trends between halo mass bins when you perform this on >10,000 halos in a large simulation volume like EAGLE as below, and I wonder if the acceleration support term would reduce many of the departures from one of the sum of support terms.

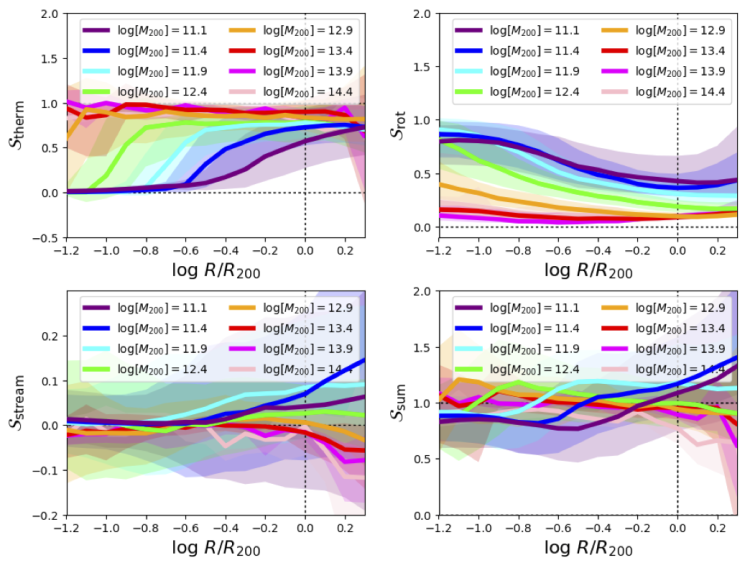
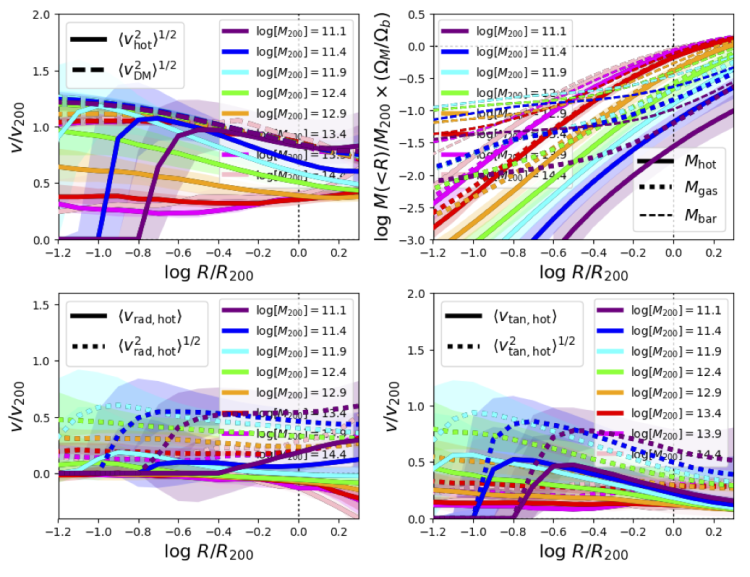
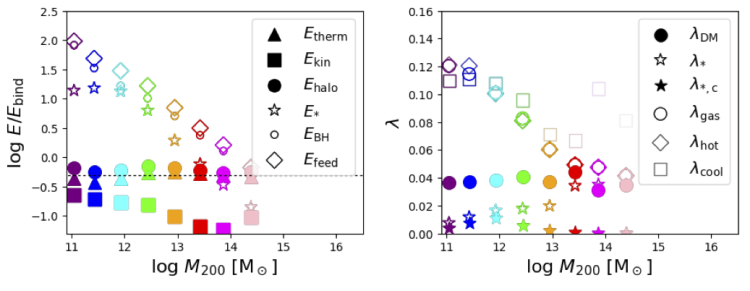
I also talk confidently in the paper about the results of a small sample of halos shown in Figures 2-5 being widely applicable to halos in general, so I did make these plots (in non-presentable versions) for the EAGLE 100 Mpc box as a check. 

Visualizations from EAGLE zooms to highlight key behaviors

Below are several visualizations created from non-equilibrium zooms that I ran at low redshift.  Many other movies have been created, but these are the ones that best show the behaviors highlighted in the paper.  Two visualizations show the same halo, first in Hydrogen and O VI, and secondly then in O VII, which traces the temperature of the inner CGM and clearly indicates net rotation of gas.  The final visualization shows AGN-driven shocks in a group halo in various filters including density, temperature, oxygen, O VI, and O VIII.